最小二乘的几何解释

1.投影与投影映射

假设$S,T$是$n-$维酉（欧氏）空间$V$的子集，且$V=S \oplus T$，其中$\oplus$代表$S,T$构成直和关系且$S,T$构成全空间$V$($V = S + T$)。对于$\forall \alpha \in V$，可唯一的表示为：
$$
\alpha = x + y, \quad x\in S, y \in T
$$

则称$x$是$\alpha$沿$T$在$S$上的投影，$y$是$\alpha$沿$S$在$T$上的投影，也称$\mathcal{T}_{S,T}:V \rightarrow S$是$V$沿着$T$至$S$的投影映射。

值得注意的是：

上式的分解是唯一的，这种唯一性是由直和决定的。所谓直和关系，即空间$S \cap T = {0}$，可以理解为构成$S,T$这两个空间的基底是线性无关的。
投影映射是线性映射，对与一个投影映射$\mathcal{T}_{S,T}$存在一个矩阵表示$A$，并且$A^2 = A$，即投影映射的矩阵表示一定是一个幂等矩阵。

唯一性的简单证明：
对于$\forall \alpha \in V$,
$$
\alpha =\mathcal{T}(\alpha) + \alpha-\mathcal{T}(\alpha), \\
\quad \mathcal{T}(\alpha) \in S, \alpha-\mathcal{T}(\alpha) \in T\\
$$
假设$\beta \in {S \cap T}$,则由于$\beta \in S$,故$\exists \gamma \in V$,使得$\beta = \mathcal{T}(\gamma)$。同理$\beta \in T$,故$\exists l\in V$,使得$\beta = l-\mathcal{T}(l)$，则:$\mathcal{T}(\gamma) = l-\mathcal{T}(l)$。对上式两端再做一次投影映射：
$$
\mathcal{T}^2(\gamma) = \mathcal{T}(l) - \mathcal{T}^2(l)=0=\beta(幂等矩阵性质)
$$
由此可见，幂等性质保证了分解是直和关系，而直和关系保证了分解是唯一的。
当上式中的$S \perp T$时，称这个投影映射为正交映射。正交映射有很多优良的性质，当为正交映射时，$T$空间中的任意向量与$S$空间中的任意向量是正交的，即$T$空间中的任意向量与$S$空间的基底是正交的。然鹅，正交投影和最小二乘又有什么关系呢？这便要说明一下高维空间的勾股定理。

2.高维空间的勾股定理

对于二维空间，我们知道三角形的斜边的平方等于两个直角边的平方和。但是这种关系在高维空间中是否还如此优美呢？这里我们要先明确一下长度的概念，向量的长度是通过内积定义的即$||\alpha||= \sqrt{<\alpha,\alpha>}=\sqrt{\alpha^H \alpha}$。现在假设在欧氏空间$V_n(R)$中，有$a,b$两个向量，那么$||a-b||^2?=?||a||^2+||b||^2$成立吗？我们计算一下长度不就可以解决了:
$$
\begin{equation}
\begin{aligned}
||a-b||^2=<a-b,a-b> &= <a,a> - <a,b> - <b,a> + <b,b>\\
&=||a||^2 - <a,b> - <b,a> + ||b||^2
\end{aligned}
\end{equation}
$$
这似乎是差了一点东西啊，那为什么勾股定理在二维空间中成立呢?这要归功于直角三角形前提，即$a,b$是垂直的，也就是正交的,这使得$ <a,b> = <b,a> = 0 $。若是在高维空间中也有这种关系，那勾股定理也就成立了。在正交映射的条件下，在$S$空间中任取$a$向量，在$T$空间中取一个$b$向量，这不天然满足正交要求吗，高维勾股定理不就天然成立了。

3.最小二乘

啰嗦了半天，重于到重点了，先放一张镇楼图.

最小二乘问题，举个例子，就是对全空间$V$中的向量$\alpha$，在$V$的子空间$W$中找到一个$\beta $,使它与$\alpha$最像，即$||\alpha-\beta||_{min}$。子空间是线性子空间的简称，它是$V$的一个非空子集，并且满足线性空间的封闭性。假设$\alpha_1,\alpha_2,...\alpha_s$是$V$中的一组向量，那么非空集合$span ( \alpha_1,\alpha_2,...\alpha_s ) = { \alpha_1k_1+\alpha_2k_2+...+\alpha_sk_s }$构成了线性空间$V$的一个子空间，而且这里的$k_i$不做要求，可以全是零。至于为什么是在子空间中寻找，我们通过后面的例子来说明。

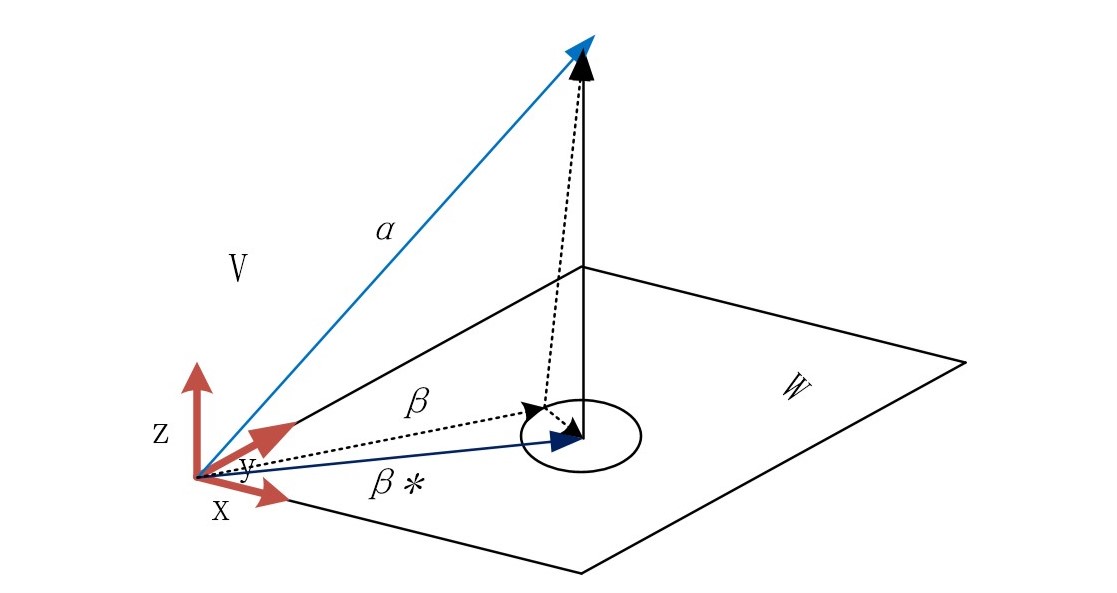
上述的重点是$||\alpha-\beta||$什么时候取到最小，如上图所示，我们可以直观的感受到:当向量$\alpha-\beta$与$W$平面垂直时，它的长度是最小的。那么对应的与$\alpha$最像的$\beta$不就是向量$\alpha$在$W$空间上的正交投影吗。用向量的语言来描述一哈，$\forall \beta \in W,当且仅当\alpha-\beta \perp W$时，$||\alpha -\beta||$是最小的。不妨来证明一下在$n$维度空间这是成立的：

设$\beta^*$是$\alpha$在$W$空间中的正交投影，$\beta$是$W$空间中的任意向量
$$
\begin{equation}
\begin{aligned}
\alpha - \beta &= \alpha - \beta^* + \beta^* - \beta \\
||\alpha-\beta||^2&=||\alpha - \beta^* + \beta^* - \beta||^2 \\
\end{aligned}
\end{equation}
$$
注意到$ \alpha - \beta^* \perp \beta^* - \beta $,由勾股定理可知:

$$
|| \alpha-\beta ||^2 = || \alpha - \beta^* ||^2 + || \beta^* - \beta ||^2
$$

因为
$$
\begin{equation}
||\beta^* - \beta||>=0 ;\\
||\alpha-\beta||^2>=||\alpha - \beta^*||^2
\end{equation}
$$

这说明$\alpha$的正交投影就是他的最小二乘解。

4.如何求解

我们知道$||\alpha-\beta||$取得最小的条件了，那求解$\beta$也就变得容易了。
选$W$空间的一组基$\phi=[\alpha_1,\alpha_2,…\alpha_m]$，在$W$空间中的任意一个向量可以表示为$\beta = [\alpha_1,\alpha_2,…\alpha_m]x$。根据最小二乘的条件，$\forall \alpha \in V,当且仅当\alpha-\beta \perp W$时，$\beta$是$\alpha$的最小二乘解。
我们前边提过，$\alpha-\beta \perp W$等价于$\alpha-\beta \perp \alpha_i,i=1,2,..m$。
于是有：
$$
\begin{equation}
\begin{aligned}
<\alpha_i,\alpha-\beta> = 0\\
<\alpha_i,\beta> = <\alpha_i,\alpha>\\
<\alpha_i,[\alpha_1,\alpha_2,…\alpha_m]x> = <\alpha_i,\alpha>\\
\left[<\alpha_i,\alpha_1>,<\alpha_i,\alpha_2>…<\alpha_i,\alpha_m>\right]x=<\alpha_i,\alpha>\\
\end{aligned}
\end{equation}
$$
在$W$中有m个$\alpha_i$,可以列出如下的方程组:
$$
\begin{equation}
\begin{aligned}
\left[
\begin{matrix}
<\alpha_1,\alpha_1>&<\alpha_1,\alpha_2>&…&<\alpha_1,\alpha_m>\\
<\alpha_2,\alpha_1>&<\alpha_2,\alpha_2>&…&<\alpha_2,\alpha_m>\\
\vdots&\vdots&\vdots&\vdots\\
<\alpha_m,\alpha_1>&<\alpha_m,\alpha_2>&…&<\alpha_m,\alpha_m>\\
\end{matrix}
\right]x=
\left[
\begin{matrix}
<\alpha_1,\alpha>\\
<\alpha_2,\alpha>\\
\vdots\\
<\alpha_m,\alpha>\\
\end{matrix}
\right]
\end{aligned}
\end{equation}
$$
上面的大矩阵在矩阵论中叫Gramian矩阵,在标准內积定义下$G(\phi)=\phi^H\phi$(H代表共轭转置),上式子记为:
$$
G(\alpha_1,\alpha_2,…\alpha_m)x = \phi^H\alpha\\
$$
于是我们得到了$\beta$在基$\phi=[\alpha_1,\alpha_2,…\alpha_m]$下的坐标$x$
从而
$$
\begin{equation}
\begin{aligned}
\beta=\phi x=\phi G^{-1}(\phi)\phi^H\alpha=\phi (\phi^H \phi)^{-1}\phi^H\alpha\\
\end{aligned}
\end{equation}
$$

5.数据拟合

有例子有真相，上边的理论怎么应用呢，我们来看一下曲线拟合的例子：

已知测量的$n$个点，$(x_1,y_1),(x_2,y_2),...(x_n,y_n)$，求做函数$y=f(x)$,达到最佳拟合效果。其中$f(x)$在一定的函数类中选取，$f(x)=k_1\varphi_1(x)+k_2\varphi_2(x)+...+k_m\varphi_m(x)$.（$\varphi(x)一般是线性无关的$，例如$\varphi_k(x)=x^{k-1}$）。

解：

$$
\begin{equation}
\begin{aligned}
y_1=&k_1\varphi_1(x_1)+k_2\varphi_2(x_1)+…+k_m\varphi_m(x_1)\\
y_2=&k_1\varphi_1(x_2)+k_2\varphi_2(x_2)+…+k_m\varphi_m(x_2)\\
\vdots\\
y_n=&k_1\varphi_1(x_n)+k_2\varphi_2(x_n)+…+k_m\varphi_m(x_n)\\
\\
\\
\left[
\begin{matrix}
y_1\\
y_2\\
\vdots\\
y_n
\end{matrix}
\right]=&
\left[
\begin{matrix}
\varphi_1(x_1)&\varphi_2(x_1) &\cdots &\varphi_m(x_1)\\
\varphi_1(x_2)&\varphi_2(x_2) &\cdots &\varphi_m(x_2)\\
\vdots&\vdots&\vdots&\vdots&\\
\varphi_1(x_n)&\varphi_2(x_n) &\cdots &\varphi_m(x_n)\\
\end{matrix}
\right]
\left[
\begin{matrix}
k_1\\
k_2\\
\vdots\\
k_m\\
\end{matrix}
\right]
\\
\\
\alpha =&
\left[
\begin{matrix}
\alpha_1& \alpha_2& \cdots& \alpha_m
\end{matrix}
\right]k=\phi k
\end{aligned}
\end{equation}
$$
曲线拟合写成了如上的向量形式，就可以和我们前边的理论对应了。这等价于在S空间$S=span( \alpha_1 \alpha_2 \cdots \alpha_m)$中找到一个
$$
\beta =
\left[
\begin{matrix}
\alpha_1& \alpha_2& \cdots& \alpha_m
\end{matrix}
\right]k
$$
使得$||\alpha-\beta||$最小，按照上面讲的公式:
$$
k=G^{-1}(\phi)\phi^H\alpha
$$
上面的公式是n个方程求解m个未知数，当n>=m时，方程才有解。就是说S空间的dim要小于n的，故而要在V的子空间中寻找解。