1、Lucas-Kanade光流
特征跟踪是指对于第一帧图像I中的像素$u = [u_x,u_y]^T$,在第二帧J中找到与其对应的像素$v=u+d=[u_x+d_x,u_y+d_y]$,我们的目标就是计算出$[d_x,d_y]$。
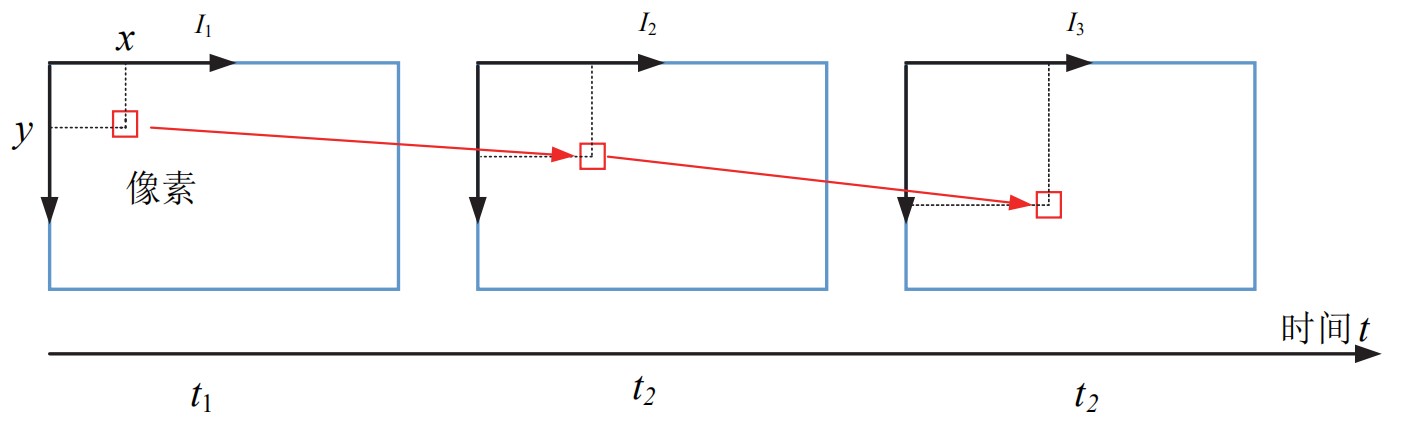
Lk光流基于灰度不变假设,并且假设同一个小窗口$w_x \times w_y$内的像素具有相同的运动,适用于运动相对平缓的场景。精确性和鲁棒性是评价特征跟踪算法的两个关键指标。
- 精度与图像的局部亚像素精度相关,直观地说,为了不“平滑”图像中包含的细节,最好使用一个小的窗口。
- 鲁棒性与光照变化、图像运动大小相关,为了处理大像素运动,直觉上最好选择一个较大窗口。
- 在选择窗口大小时,在局部精度和鲁棒性之间存在自然的折衷。
LK光流的具体推导在高翔的《视觉SLAM十四讲》中详细给出,思路清晰,步骤简单,这里不再列出。本篇主要记录以迭代的方式推导LK光流,以及LK光流的改进算法–金字塔LK光流。
2、Image pyramid representation
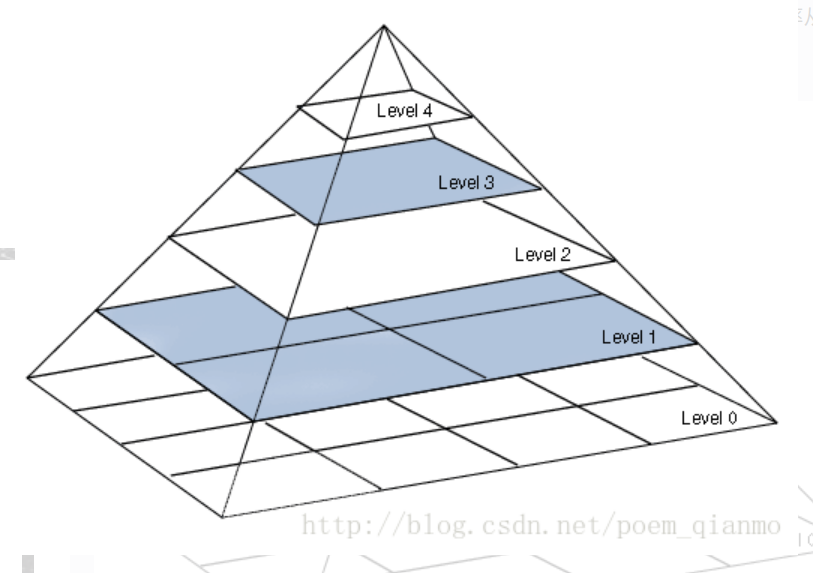
图像金字塔使用迭代的方式表示,第0层是原始的图像$I_0$大小为$n_x\times n_y$,第1层由第0层计算而来,第2层由第1层计算而来…。这样第L层的图像$I^L$,有如下的迭代表示:
$$\begin{aligned}
I^{L}(x, y)=& \frac{1}{4} I^{L-1}(2 x, 2 y)+\\
& \frac{1}{8}\left(I^{L-1}(2 x-1,2 y)+I^{L-1}(2 x+1,2 y)+I^{L-1}(2 x, 2 y-1)+I^{L-1}(2 x, 2 y+1)\right)+\\
& \frac{1}{16}\left(I^{L-1}(2 x-1,2 y-1)+I^{L-1}(2 x+1,2 y+1)+I^{L-1}(2 x-1,2 y+1)+I^{L-1}(2 x+1,2 y+1)\right)
\end{aligned}$$
上述公式只在$0\leq 2x \leq n_x^{L-1}-1$, $0\leq 2x \leq n_x^{L-1}-1$时有定义,它表明第L-1层的图像经过平滑和亚采样就可以得到第L层的图像。一般情况下,金字塔的层数不超过4层,一个640x480大小的图像,第一、第二、第三、第四层的大小分别是320x240,160x120,80x60,40x30。引入图形金字塔的目的是能够处理大像素(large pixel motions)的运动(大于窗口$w_x$和$w_y$)。
定义$u^L=[u_x^L,u_y^L]$是一个给定的点在第L层图像上的像素坐标,向量$u^L$可以通过下面的公式计算:
$$
u^L = \frac{u}{2^L}; u = u^0
$$
3、Pyramidal Feature Tracking
金字塔跟踪算法概述如下:1、在顶层$L_m$计算光流,得到跟踪的结果;2、计算的结果传导到下一层$L_{m-1}$,作为本层计算的初始值,调整光流计算,并将结果传递给下一层;3、重复此计算流程,直到$L_0$层。
我们使用数学来描述L+1层与L层之间的递推关系,假设第L层的光流计算初始值是$g^L = [g_x^L,g_y^L]$。为了计算第L层的光流,有必要找到使新的图像匹配误差函数$\epsilon^{L}\left(\mathbf{d}^{L}\right)$最小化的像素位移矢量$d^L=[d_x^L,d_y^L]$:
$$
\epsilon^{L}\left(\mathbf{d}^{L}\right)=\epsilon^{L}\left(d_{x}^{L}, d_{y}^{L}\right)= \sum_{x=u_{x}^{L}-\omega_{x}}^{u_{x}^{L}+\omega_{x}} \sum_{y=u_{y}^{L}-\omega_{y}}^{u_{y}^{L}+\omega_{y}}\left(I^{L}(x, y)-J^{L}\left(x+g_{x}^{L}+d_{x}^{L}, y+g_{y}^{L}+d_{y}^{L}\right)\right)^{2}
$$
这个公式是最小化光度误差,注意,初始值向量$g^L$用于预挪移(pre-translate)第二帧图像J中的图像块。这样,残余像素向量$d^L=[d_x^L,d_y^L]^T$很小,因此很容易通过标准的Lucas-Kanade步骤进行计算,迭代的Lucas-Kanade算法在下一节给出,它将用来计算$d^L=[d_x^L,d_y^L]^T$,现在假设$d^L=[d_x^L,d_y^L]^T$已经被计算出来。然后,本层(第L层)的计算结果传导给下一层(第L-1层),作为L-1层光流计算的初始值$g^{L-1}$:
$$
g^{L-1} = 2(g^L+d^L) \tag{3.1}
$$
下一层的像素残差剩余向量经过同样的步骤,通过最小化$\epsilon^{L-1}\left(\mathbf{d}^{L-1}\right)$获得结果$d^{L-1}$。算法通过将$L_m$层的初始值设置为零来初始化(金字塔最高层没有可用的初始值):
$$
g^{L_m} = [0,0]^T
$$
迭代计算到最底层便得到最后的结果:
$$
d = g^0+d^0 = \sum_{L=0}^{L_m}2^Ld^L
$$
金字塔实现的明显优点是,在计算大的整体像素位移矢量$d$时,每个剩余光流矢量$d^L$可以保持非常小。
4、Iterative Lucas-Kanade
4.1、standard version
在第3节中,我们得出对于每一金字塔层,目标是找出使匹配代价函数$\epsilon^{L}$最小化的$d^L$。我们用A和B代表两帧图像:
$$
A(x, y) \doteq I^{L}\left(x, y\right) \\
B(x, y) \doteq J^{L}\left(x+g_{x}^{L}, y+g_{y}^{L}\right)
$$
为了清晰起见,我们使用$\bar{\nu}=[v_x,v_y]^T$来表示$d^L$,使用$p=[p_x,p_y]^T$来表示$u^T$。使用新的符号表示后,我们的目标是选择向量$\bar{\nu}=[v_x,v_y]^T$使得匹配代价函数最小:
$$
\varepsilon(\bar{\nu})=\varepsilon\left(\nu_{x}, \nu_{y}\right)=\sum_{x=p_{x}-\omega_{x}}^{p_x+w_x} \sum_{y=p_{y}-\omega_{y}}^{p_{y}+\omega_{y}}\left(A(x, y)-B\left(x+\nu_{x}, y+\nu_{y}\right)\right)^{2} \tag{4.1.1}
$$
处理的思路是求解公式(4.1.1)导数为0的点,具体的处理步骤如下,首先公式(4.1)对变量$\bar{\nu}=[v_x,v_y]^T$求导,结果如下:
$$
\frac{\partial \varepsilon(\bar{\nu})}{\partial \bar{\nu}}=-2 \sum_{x=p_{x}-\omega_{x}}^{p_x+w_x} \sum_{y=p_{y}-\omega_{y}}^{p_{y}+\omega_{y}}\left(A(x, y)-B\left(x+\nu_{x}, y+\nu_{y}\right)\right) \cdot\left[\begin{array}{cc}
\frac{\partial B}{\partial x} & \frac{\partial B}{\partial y}
\end{array}\right] \tag{4.1.2}
$$
在$\bar{\nu}=[0,0]^T$处,对$B(x+v_x,y+v_y)$一阶泰勒展开,由于我们引入了金字塔处理(第3节),$\bar{\nu}$比较小,泰勒展开没得毛病。进行处理后,公式(4.1.2)近似为:
$$
\frac{\partial \varepsilon(\bar{\nu})}{\partial \bar{\nu}}=-2 \sum_{x=p_{x}-\omega_{x}}^{p_x+w_x} \sum_{y=p_{y}-\omega_{y}}^{p_{y}+\omega_{y}}\left(A(x, y)-B\left(x, y\right)-\left[\begin{array}{cc}
\frac{\partial B}{\partial x} & \frac{\partial B}{\partial y}
\end{array}\right]\bar{\nu}\right) \cdot\left[\begin{array}{cc}
\frac{\partial B}{\partial x} & \frac{\partial B}{\partial y}
\end{array}\right] \tag{4.1.3}
$$
$A(x,y)-B(x,y)$可以解释为在点$[x,y]^T$处的图像时间导数(temporal image derivative),$\left[\begin{array}{cc}
\frac{\partial B}{\partial x} & \frac{\partial B}{\partial y}
\end{array}\right]$是图像的像素梯度,我们标记为:
$$
\delta I(x,y) \doteq A(x,y) - B(x,y) \\
\nabla I=\left[\begin{array}{c}
I_{x} \\
I_{y}
\end{array}\right] \doteq\left[\begin{array}{cc}
\frac{\partial B}{\partial x} & \frac{\partial B}{\partial y}
\end{array}\right]^{T}
$$
$I_x$和$I_y$可以直接通过图像A(x,y)(不是B(x,y))直接计算出来,这里选择中心差分算子:
$$
\begin{aligned}
&I_{x}(x, y)=\frac{\partial A(x, y)}{\partial x}=\frac{A(x+1, y)-A(x-1, y)}{2}\\
&I_{y}(x, y)=\frac{\partial A(x, y)}{\partial y}=\frac{A(x, y+1)-A(x, y-1)}{2}
\end{aligned}
$$
整理后,公式(4.1.3)可以写为:
$$
\frac{1}{2} \frac{\partial \varepsilon(\bar{\nu})}{\partial \bar{\nu}} \approx \sum_{x=p_{x}-\omega_{x}}^{p_x+w_x} \sum_{y=p_{y}-\omega_{y}}^{p_{y}+\omega_{y}}\left(\nabla I^{T} \bar{\nu}-\delta I\right) \nabla I^{T} \\
$$
$$
\frac{1}{2}\left[\frac{\partial \varepsilon(\bar{\nu})}{\partial \bar{\nu}}\right]^{T} \approx \sum_{x=p_{x}-\omega_{x}}^{p_x+w_x} \sum_{y=p_{y}-\omega_{y}}^{p_{y}+\omega_{y}}\left(\left[\begin{array}{cc}
I_{x}^{2} & I_{x} I_{y} \\
I_{x} I_{y} & I_{y}^{2}
\end{array}\right] \bar{\nu}-\left[\begin{array}{c}
\delta I I_{x} \\
\delta I I_{y}
\end{array}\right]\right)
$$
Denote:
$$
G \doteq \sum_{x=p_{x}-\omega_{x}}^{p_x+w_x} \sum_{y=p_{y}-\omega_{y}}^{p_{y}+\omega_{y}}\left[\begin{array}{cc} I_{x}^{2} & I_{x} I_{y}, \\
I_{x} I_{y} & I_{y}^{2}\end{array}\right]
\bar{b} = \sum_{x=p_{x}-\omega_{x}}^{p_x+w_x} \sum_{y=p_{y}-\omega_{y}}^{p_{y}+\omega_{y}}\left[\begin{array}{c}
\delta I I_{x} \\
\delta I I_{y}
\end{array}\right]
$$
最后的方程可以简化为:
$$
\frac{1}{2}\left[\frac{\partial \varepsilon(\bar{\nu})}{\partial \bar{\nu}}\right]^{T} \approx G \bar{\nu}-\bar{b}
$$
最优的光流向量是:
$$
\bar{\nu}_{opt} = G^{-1}\bar{b} \tag{4.1.4}
$$
当矩阵G是可逆的,则这个结果是有意义的。这表明$p$点周围的像素在$x$,$y$方向都需要具有梯度信息。以上是标准的Lucas-Kanade光流算法,只有当像素位移很小时才有效(为了满足一阶泰勒展开)。
4.2、iterative version
我们用$k$表示迭代次数,$k$从1开始。使用迭代的方式来描述算法,假若第1、2、3……$k-1$次的计算结果为第$k$次的计算提供了一个初始值$\bar{v}^{k-1}=[v_x^{k-1},v_y^{k-1}]$。$B_k$是第$k$次迭代的挪移后的图像(translated image),它根据原始图像$B(x,y)$与初始值生成:
$$
B_k(x,y)=B(x+v_x^{k-1},y+v_y^{k-1})
$$
我们的目标是计算出剩余像素位移矢量(residual pixel motion vector)$\bar{\eta}^k=[\eta_x^k,\eta_y^k]$,使得下面的光度误差函数最小:
$$
\varepsilon^{k}\left(\bar{\eta}^{k}\right)=\varepsilon\left(\eta_{x}^{k}, \eta_{y}^{k}\right)=\sum_{x=p_{x}-\omega_{x}}^{p_x+w_x} \sum_{y=p_{y}-\omega_{y}}^{p_{y}+\omega_{y}}\left(A(x, y)-B_{k}\left(x+\eta_{x}^{k}, y+\eta_{y}^{k}\right)\right)^{2}
$$
这个误差最小化函数的解可以通过一步Lucas-Kanade算法(第4.1.1节)计算出:
$$
\bar{\eta}^k=G^{-1}\bar{b}_k
$$
$\bar{b}_k$是一个2x1的向量,每次迭代的数值都在变,而矩阵G通常情况下只需要计算一次。
$$
\bar{b}{k}=\sum{x=p_{x}-\omega_{x}}^{p_{x}+\omega_{x}}\sum_{y=p_{y}-\omega_{y}}^{p_{y}+\omega_{y}}
\left[\begin{array}{c}
\delta I_{k}(x, y) I_{x}(x, y) \\
\delta I_{k}(x, y) I_{y}(x, y)
\end{array}\right]
$$
其中:
$$
\delta I_k(x,y) = A(x,y)-B_k(x,y)
$$
于是对于第k+1次的迭代计算,它的初始值为:
$$
\bar{v}^k=\bar{v}^{k-1}+\bar{\eta}^k
$$
这样便继续迭代下去,对于第一次迭代(k=1),我们设其迭代初始值为:$\bar{\nu}^0=[0,0]^T$。假设K次迭代达到收敛,则光流矢量的最终解为:
$$
\bar{v}=d^L=\bar{v}^K=\sum_{k=1}^{K}\bar{\eta}^k
$$
将向量$d^L$馈送到方程(3.1),并且在所有的金字塔层L-1、L-2,…,0重复整个过程。
5、Summary

6、Details
6.1、detail 1
在计算的过程中,像素可能不是整数,这时候我们通过双线性差值来计算亮度:
$$
\begin{aligned}
I^{L}(x, y)=&\left(1-\alpha_{x}\right)\left(1-\alpha_{y}\right) I^{L}\left(x_{o}, y_{o}\right)+\alpha_{x}\left(1-\alpha_{y}\right) I^{L}\left(x_{o}+1, y_{o}\right)+\\
&\left(1-\alpha_{x}\right) \alpha_{y} I^{L}\left(x_{o}, y_{o}+1\right)+\alpha_{x} \alpha_{y} I^{L}\left(x_{o}+1, y_{o}+1\right)
\end{aligned}
$$
其中$x_0$,$y_o$是$x$与$y$的整数部分:
$$
x=x_0+\alpha_x\\
y=y_0+\alpha_y
$$
6.2、detail 2
当要跟踪的点在图像的边缘,这时候若强制要求每层的金字塔窗口$w_x \times w_y$内的像素都有效,在最低层就会有很大一片区域无法光流追踪。假设我们取窗口大小$w_x=w_y=5$,金字塔层数$L_m = 3$,则在最底层距离边缘$2^3\times5=40$像素的区域不能用来光流跟踪。
为了防止这种情况的发生,我们可以保留部分窗口中的像素点在图像之外(在任何金字塔级别)的情形。这种情况下,在Summary部分对应的流程中,只有带有求和符号的公式需要改动,其余公式不需要该改变。所有窗口内的点都落在图像中时,我们只需要计算一次矩阵G;对于边缘区域,每次迭代都要重新计算矩阵G。
6.3、detail 3
当出现以下的情形时,我们可以判定光流跟踪失败:
- 像素点落在了图像外;
- 图像I和图像J之间跟踪点周围的图像块灰度变化过大(该点由于遮挡而消失)。
对于第二种情况,我们可以设定光度误差函数要大于一个阈值,但是这个阈值比较难选取,关于这部分的详细讲解请参考参考文献。
7、Feature Selection
在求解向量$d^l$时,只有当矩阵G是可逆的,公式(4.1.4)才有意义,换句话说矩阵G的最小特征值要足够大。因此对特征点的选取有一定的要求,一个选取good feature的步骤可以是:
- 计算图像I中每个像素处的G矩阵及其最小特征值$\lambda_m$。
- 记$\lambda_{max}$为整个图像上$\lambda_m$的最大值。
- 保留图像像素中$\lambda_m$大于$\lambda_{max}$一定百分比的像素,该百分比可以是10%或5%。
- 从这些像素中,保留局部最大像素(如果像素的$ \lambda_m $值大于其3×3邻域中任何其他像素的,则保留该像素)。
- 将这些点稀疏化,使像素对之间的最小距离大于给定的阈值距离(例如10或5像素)。(可选步骤)
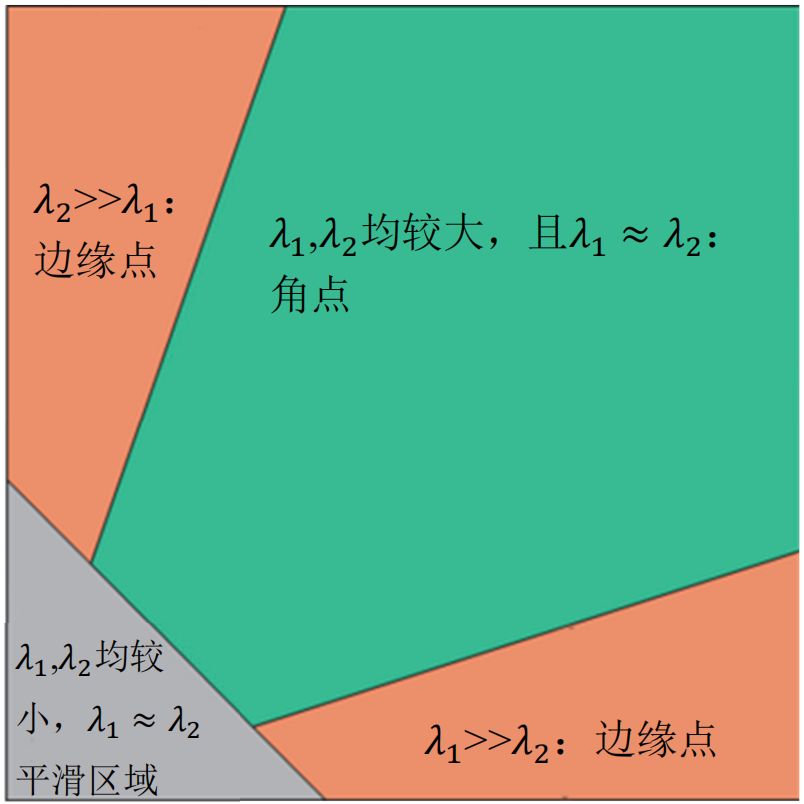
以上步骤中最重要的是要尽可能保证矩阵G可逆,我们注意到Harris角点便能满足这一点,Harris角点选取的依据是判断如下矩阵$M_H$的特征值,其中$w(x,y)$是权值函数:
$$
M_{H}=\sum_{x, y} w(x, y)\left[\begin{array}{cc}
I_{x}^{2} & I_{x} I_{y} \\
I_{x} I_{y} & I_{y}^{2}
\end{array}\right]
$$
Harris角点选取:
8、Reference
《视觉SLAM十四讲从理论到实践》
Pyramidal Implementation of the Lucas Kanade Feature Tracker Description of the algorithm

