多视图三角化
在介绍三角化之前,我们先引入一个符号“^”。通常我们通过下面的公式计算两个向量的叉乘(外积):
$$
\boldsymbol{a} \times \boldsymbol{b}=\left[\begin{array}{ccc}
\boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k} \\
a_{1} & a_{2} & a_{3} \\
b_{1} & b_{2} & b_{3}
\end{array}\right]=\left[\begin{array}{c}
a_{2} b_{3}-a_{3} b_{2} \\
a_{3} b_{1}-a_{1} b_{3} \\
a_{1} b_{2}-a_{2} b_{1}
\end{array}\right]=\left[\begin{array}{ccc}
0 & -a_{3} & a_{2} \\
a_{3} & 0 & -a_{1} \\
-a_{2} & a_{1} & 0
\end{array}\right] \boldsymbol{b} \triangleq \boldsymbol{a}^{\wedge} \boldsymbol{b}
$$
引入“^”符号后,把$a$写成矩阵,实际上是一个反对称矩阵,如此就把外积$a \times b$写成了矩阵与向量的乘法$a^{\wedge}b$。
1、两视图三角化
在单目SLAM中,仅通过单张图像我们无法获得像素的深度信息,这时候需要通过三角测量的方法来估计地图点的深度。三角测量是指:通过在两处观察同一个点的夹角,确定该点的距离。
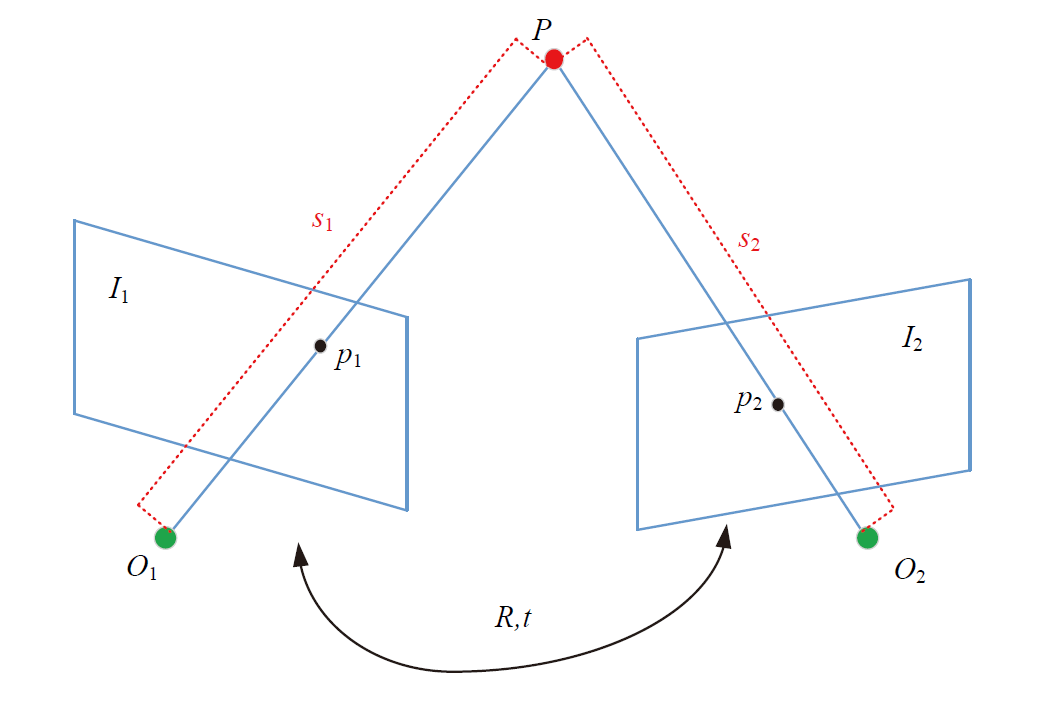
考虑$I_1$,$I_2$两帧图像,$R,t$是第二帧相对于第一帧的旋转矩阵和平移向量(对应的变换矩阵是$T_{12}$)。在$I_1$中有特征点$p_1$,对应于$I_2$中的匹配点$p_2$。根据相机的内参数矩阵$K$,我们便可以获得$p_1$在$I_1$帧归一化图像平面中的点$x_1=K^{-1}p_1$;$p_2$在$I_2$帧归一化平面中的点$x_2=K^{-1}p_2$。
根据对极约束,他们满足如下的关系:
$$
s_1x_1 = s_2Rx_2+t \tag{1.1}
$$
先对公式(1.1)左右两端左乘$x_1^{\wedge}$,得到:
$$
s_1x_1^{\wedge}x_1 = 0 = s_2x_1^{\wedge}Rx_2+x_1^{\wedge}t
\tag{1.2}
$$
根据公式(1.2)的右端,可以计算出$s_2$,进而根据公式(1.1)计算出$s_1$,我们便可得到路标点$P$在这两帧中的深度。然而,在实际的位姿估计中,我们估计的值往往存在误差,公式(1.2)不严格为0。这时候我们可以计算最小二乘解,参见最小二乘的几何解释
2、多视图三角化
在滑动窗口中,路标点经常被多个关键帧同时观测,考虑路标点$Y$,在多个关键帧$k=1,…,n$中观测到。
为了计算方便我们取$Y \in \mathbb{R}^4$,在每一帧中的观测取归一化平面坐标$x_k=[u_k,v_k,1]^T$(与像素坐标只差一个相机内参)。
记投影矩阵$P_k=[R_k,t_k] \in \mathbb{R}^{3\times4}$,为World坐标系到Camera坐标系的变换。有如下的投影关系:
$$
\forall k,\lambda_kx_k=P_kY
\tag{2.1}
$$
展开:
$$
\lambda_k\left[\begin{array}{ccc}
u_k \\
v_k\\
1
\end{array}\right]
=\left[\begin{array}{ccc}
P_{k,1}^T \\
P_{k,2}^T \\
P_{k,3}^T
\end{array}\right]Y
\tag{2.2}
$$
根据公式(2.2)的第三行有:$\lambda_k=P_{k,3}^TY$,其中$P_{k,3}^T$是$P_k$的第3行。
将第三行的结果带入前两行则有:
$$
u_kP_{k,3}^TY = P_{k,1}^TY
$$
$$
v_kP_{k,3}^TY = P_{k,2}^TY
\tag{2.3}
$$
每次的观测都会提供两个这样的方程,$Y$是未知量,将$Y$移动到等式的另一侧:
$$
\left[\begin{array}{c}
u_{1} P_{1,3}^T-P_{1,1}^T \\
v_{1} P_{1,3}^T-P_{1,2}^T \\
\vdots \\
u_{n} P_{n, 3}^T-P_{n, 1}^T \\
v_{n} P_{n, 3}^T-P_{n, 2}^T
\end{array}\right] Y=0 \rightarrow \mathbf{D} Y=0
\tag{2.5}
$$
这就转换成了变量长度一定时的优化问题,关于这个方程的求解,可以阅读这篇文章AX=0的最小二乘解

