矩阵分解理论
本节主要记录常用的矩阵分解,知识主要来源于上学期所学的矩阵分析课程。不同于大多数的博客,我这里主要在复线性空间和酉空间中讨论。没有矩阵分析基础的同学,文章前边的一些内容看起来会比较晦涩,但是学过线代看明白矩阵分解部分的内容是不成问题的。
1、线性映射
线性映射的定义:

当入口空间和出口空间是同一个时,线性映射就是线性变换。线性映射的性质:

有限维线性空间上线性映射的矩阵表示:

有了矩阵表示的定义以及线性映射的性质,我们可以推出下面的公式:

$AP=QB$这个公式的几何意义:任意线性映射都可以通过重新选入口基和出口基的方式,将矩阵表示化简。在下面的小节中我会不断地提及这句话。
2、特殊矩阵
2.1、Hermite矩阵
$A \in \mathbb{C}^{n \times n}$,若$A^H=A$,($H$代表共轭转置),称$A$为Hermite矩阵,若$A^H=-A$,则称$A$为反Hermite矩阵。$H$矩阵的对角线元素的虚部为零。
对于Hermite矩阵$A$,有$\forall x \in \mathbb{C}^{n}$,$x^HAx \geq 0$,这说明Hermite矩阵是正半定,若$A$非奇异,则$A$是正定的。
对于Hermite矩阵$B$,若$B$同时还是一个上(下)三角矩阵,则$B$是对角阵。
2.2、酉矩阵
设$A$是一个$n$-阶复矩阵,如果其满足:
$$
A^HA = AA^H=I
$$
则称$A$是酉矩阵,一般记为$A \in U^{n \times n}$。我们常说的旋转矩阵,就是酉矩阵。
设$A,B \in U^{n \times n}$,有如下的性质:
- $A^{-1} = A^H \in U^{n \times n}$;
- $|det(A)|=1$;
- $AB,BA \in U^{n \times n}$。
$A$是一个酉矩阵的充分必要条件是$A$的$n$个列(或行)向量组是一个(标准内积意义下的)标准正交向量组。
酉矩阵的列向量组是该空间的一个标准正交基。(因为内积度量矩阵Gramian矩阵等于$I$),从变换的角度考虑,酉变换意味着坐标的旋转($det(A)=1$)或者镜像($det(A)=-1$),变换前后不改变内积,既不改变向量的大小,也不改变向量的夹角关系:
$$
<Ux,Uy>=x^HU^HUy=x^Hy=<x,y>
$$
若矩阵$A$即是酉矩阵又是上(下)三角矩阵,则$A$是单位矩阵。简单的证明:因为$A$是上三角矩阵,所以$A^{-1}$是上三角矩阵,又因为$A^{-1}=A^H$,所以$A^{-1}$又是下三角矩阵,所以$A$是对角阵,进而是单位矩阵。
2.3、正规矩阵
设$A \in \mathbb{C}^{n \times n}$,如果$A$满足:
$$
A^HA=AA^H
$$
则称$A$是正规矩阵,对角矩阵,Hermite矩阵,酉矩阵都是正规矩阵。
若$A$是正规矩阵,且$A$是上三角矩阵,则$A$是对角矩阵。
3、常用矩阵分解
3.1 Jordan分解
Jordan标准型在线性代数中涉及的比较少,在矩阵分析中引入了$\lambda-$矩阵后,便比较好理解了,这里直接给出一些结论:
由Jordan标准形存在定理可知,复数域上,任意一个方阵A总可以找到非奇异矩阵P,使得:
$$
AP=PJ
$$
这里$J$是Jordan标准型,这意味着$A$相似于$P$。
值得注意的是:上述是在$\mathbb{C}$空间上讨论问题,即是$A \in \mathbb{R}^{n \times n}$,$J$和$P$也仍然在$\mathbb{C}^{n \times n}$中。
3.2 正交化方法与QR分解
若$\alpha , \beta$是$V$空间中的向量,则$\alpha$在$\beta$上的正交投影$\gamma$是:
$$
\gamma = \frac{\beta}{||\beta||}||\alpha|| \frac{<\alpha,\beta>}{||\alpha|| \cdot ||\beta||}
=\frac{\beta}{||\beta||}<\frac{\beta}{||\beta||},\alpha>
$$
上面的公式是由单位方向矢量和模长两部分组成,用到了向量之间的夹角公式。
那么如何由一组线性无关的向量组,构造出一个标准的正交向量组?这需要使用到Schmidt正交化方法:

将上图中的公式移项处理:

最后一个公式的几何意义为:由$A=[\alpha_1,\alpha_2,…\alpha_n]$的各列递推构造一个标准正交基,并将$A$的各列重新表示为这个基的线性组合。
于是我们便得出了QR(正交-上三角)分解:
任意非奇异方阵$A \in \mathbb{C}^{n \times n}$,必然可以唯一分解为$A=QR$其中$Q$为酉矩阵,$R$是正线(对角线元素为正数)上三角矩阵。
值得注意的是:在Schmidt正交化过程中,我们是从矩阵$A$的第一列元素递推到最后一列元素,我们当然也可以从最后一列开始Schmidt正交化,这样得到的分解结果是一个酉矩阵乘一个正线下三角。
3.3、酉相似
设$A,B \in \mathbb{C}^{n \times n}$或者($\mathbb{R}^{n \times n}$),若存在$U \in U^{n \times n}$使得
$$
U^HAU = U^{-1}AU=B
$$
则称$A$与$B$酉相似($A$酉相似于$B$)。
任何一个$n-$阶复矩阵$A$酉相似于一个上(下)三角矩阵,证明如下:
由Jordan分解得到:$\exists P \in \mathbb{C}^{n \times n}$,$A = PJP^{-1}$;$P$是非奇异的。
由QR分解得$P=QR$,带入得到$A=Q(RJR^{-1})Q^H$。
这个定理说明:任意线性变换都能够通过重新选取标准正交坐标系,简化表示矩阵。
对于正规矩阵,酉相似有更特殊的性质:

在此基础上,我们有如下的推论:

3.4、奇异值分解
3.4.1、奇异值的定义及SVD分解:

若矩阵$A$是Hermite矩阵,则$A$的特征值就是它的奇异值。
SVD分解:

对于最后一句话,我们可以这样理解:
$AA^H$是一个Hermite矩阵,他酉相似于一个对角阵,根据3.3节,我们知道这个对角阵中对角线元素是$AA^H$的特征值,也就是矩阵$A$奇异值的平方。对此对于左奇异值矩阵$U$,有如下的关系:
$$
AA^H = UDD^HU^H
$$
同理对于右奇异值矩阵,有如下关系:
$$
A^HA = VD^HDV^H
$$
需要指出的是,这里$DD^H$与$D^HD$在矩阵的角度上不相同,因为他们的维度不同,但是他们在主对角线的奇异值是相等的。
SVD分解的几何意义:在入口和出口空间重新选取标准正交基,可以将任意线性变换的矩阵表示简化为对角矩阵。由于酉变换不改变标准长度,此分解揭示了线性变换的本质:沿着某正交坐标轴伸缩。
3.4.2、SVD分解的低秩逼近
设矩阵$X \in \mathbb{C}^{m \times n}$,秩为$r$,$r \leq min(m,n)$,则该矩阵可以分解为:
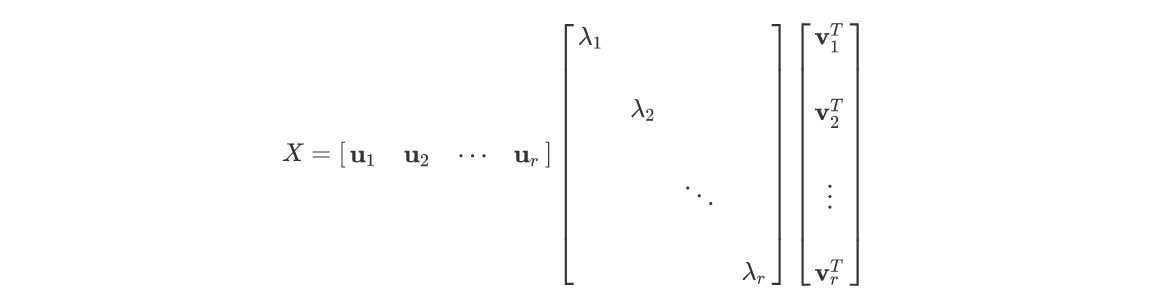
也可以表示为:($\lambda$从大到小排列)
$$
X=\sum_{i=1}^{r}\lambda_i \mathbf{u}_i \mathbf{v}_i^T
$$
低秩逼近是指:
$$
X \approx \widetilde{X} = \sum_{i=1}^{k}\lambda_iu_iv_i^T,k \leq r
$$

