IMU预积分技术(一)
IMU预积分技术最早由Todd Lupton和Salah Sukkarieh在2012年提出,C Forster等在2015年将其扩展到李代数上。IMU预积分的初衷,是将帧与帧之间的IMU相对测量信息转换为约束载体姿态的边加入到优化框架中来。为了对VIO有更清晰的认识,特将IMU预积分的经典文献做了整理。这篇文章的内容主要来自Visual-Inertial-Aided Navigation for High-Dynamic Motion in Built Environments Without Initial Conditions。
1、全局固定坐标系下的惯性导航
1.1、全局坐标系下的惯性导航
IMU最初是在航天领域被开发和应用的,在这种应用场景下,经常在全局参考的固定的导航框架中计算导航解。惯性导航的核心原理是牛顿第二定律:加速度的积分是速度,速度的积分是位移。
陀螺仪和加速度计的量测:是相对于惯性空间的测量值在载体坐标系下的投影。在Globally referenced的frame中积分计算导航解时,IMU测量值首先需要被转换到Globally regerenced的参考系下。为了完成这个转换,我们需要获取载体在Globally frame中的初始位置和姿态,以及加速度二次积分过程中需要的初始速度(这也被称为初始条件要求)。这个过程可用如下的图片说明:
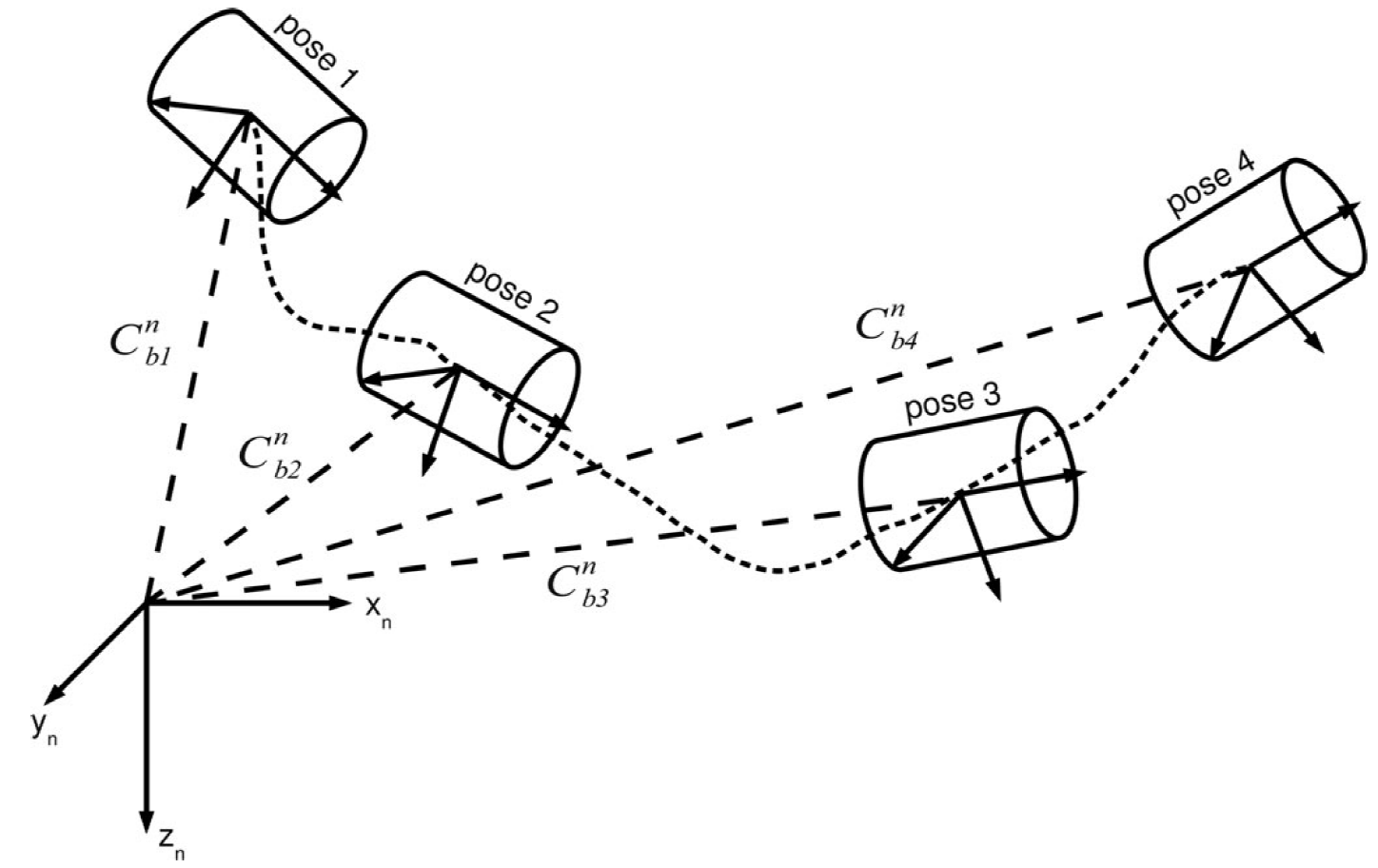
点线表示飞行器的轨迹和在这些点的惯性测量值,惯性观测被转换成由点划线显示的Globally referenced导航参考系下。
初始条件在补偿重力时显得尤其重要,一个最简单的初始化方法是将载体置于已知的位置、速度和姿态下,并将其用作起点。
不同于航空航天等应用场景,SLAM主要应用于小规模的定位,这意味着地球的曲率可以忽略,同时SLAM一般使用低成本的IMU,这样地球的自转就不会产生显著的影响。因此,我们不必进行复杂的惯导姿态解算:
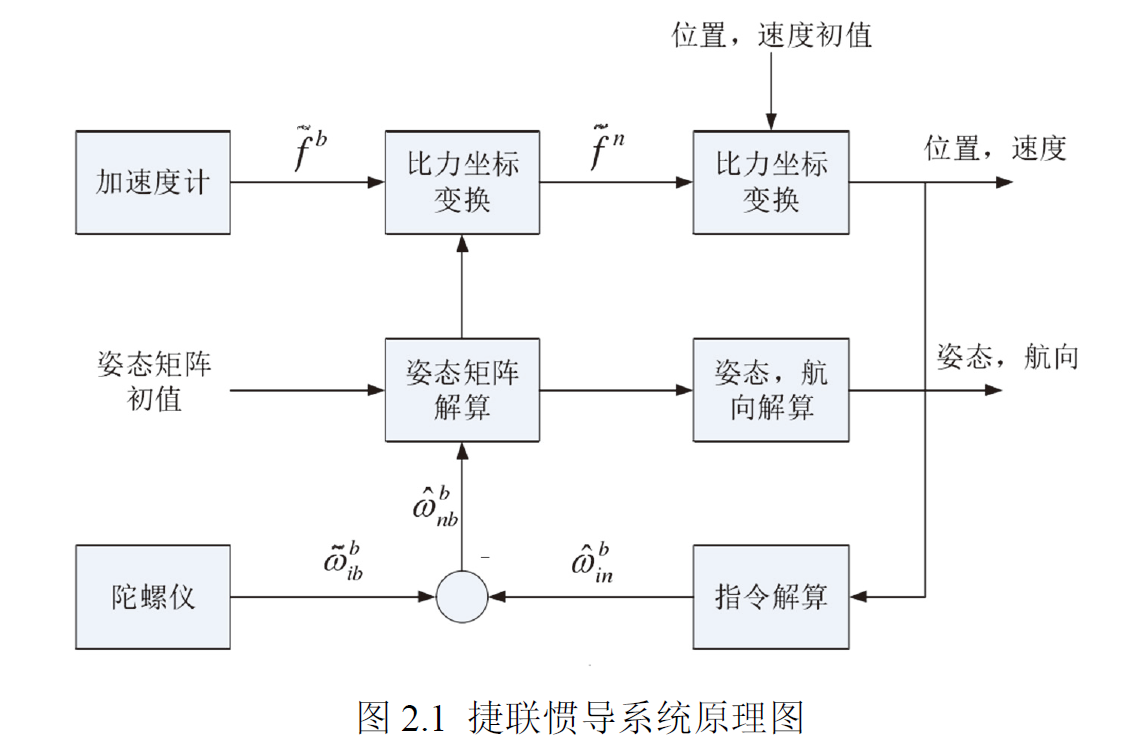
1.2、IMU器件模型
这时候IMU器件的测量模型可以简化:
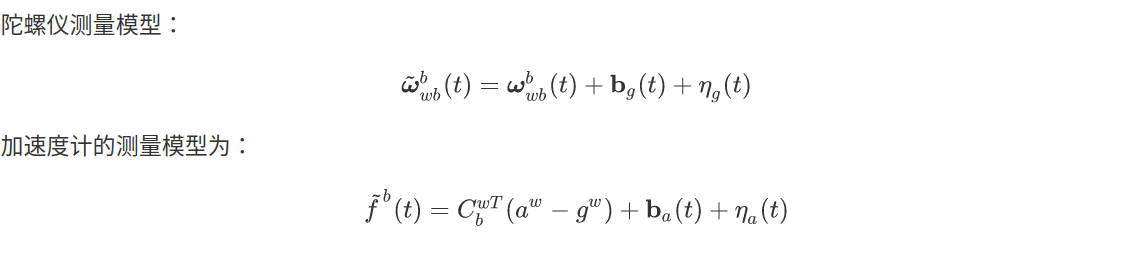
其中$\mathbf{b_g}$与$\mathbf{b_a}$是随时间缓慢变化的陀螺仪与加速度计的bias;在VINS-mono中被建模为随机游走——即$\mathbf{b_g}$与$\mathbf{b_a}$的导数服从高斯分布:
.png)
其中$C_{b t}^{n}$与$E_{b t}^{n}$分别是从当前载体姿态旋转到导航坐标系下的旋转$\phi_{t}^{n}$对应的旋转与旋转速率矩阵。
使用欧拉积分,并建立匀速运动模型,我们可以得到连续积分公式(1.1)最简单的离散形式,算法如下:

对于SLAM,我们不只是需要下一时刻积分后的解,还需获得解的不确定性,这样当与其他传感器融合时,我们可以对它们进行加权,从而给出载体姿态的最优估计。那么这个不确定性也就是协方差矩阵,该怎样随着Algorithm 1中的递推关系式计算出呢?
1.3、不确定性的计算
已知一个变量$y=Ax,x \sim \mathcal{N}(0,\Sigma_x)$,则有$\Sigma_y$:
$$
\Sigma_y=E((Ax)(Ax)^T)=E(Axx^TA^T)=A\Sigma_xA^T
$$
假设已知相邻时刻状态误差的线性递推传递方程:
$$
\delta x_{k}=F_{k-1} \delta x_{k-1}+G_{k-1}\eta_{k-1} \tag{1.2}
$$
例如状态量误差为$\delta x_k=[\delta p_k,\delta v_k,\delta \phi_k]$,测量噪声$\eta_k=[\eta_k^g,\eta_k^a]$。误差的传递由两部分组成:当前时刻传递给下一时刻的,当前时刻测量噪声传递给下一时刻的。协方差矩阵可以通过递推计算得到:
$$
\Sigma_{k}=F_{k-1}\Sigma_{k-1}F_{k-1}^T+G_{k-1}\Sigma_nG_{k-1}^T \tag{1.3}
$$
其中$\Sigma_n$是测量噪声的协方差矩阵,协方差从初始时刻0开始递推$\Sigma_0=\mathbf{0}$。
通常对于状态量之间的递推关系是非线性方程如$x_k=f(x_{k-1},u_{k-1})$,其中状态量是$x$,$u$是系统的输入量。我们可以用两种方法来推导状态误差传递的线性递推关系:
- 基于一阶泰勒展开的误差递推方程;
- 基于误差随时间变化的递推方程。
1.3.1、基于一阶泰勒展开的误差递推方程
令状态量为$x=\hat{x}+\delta x$,其中$\hat{x}$是真实值,$\delta x$是误差。对状态之间的非线性递推方程$x_k=f(x_{k-1},u_{k-1})$进行一阶泰勒展开:
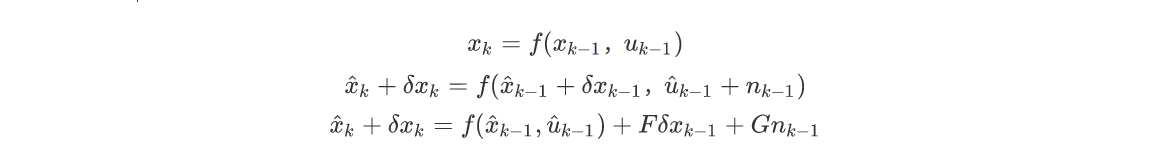
由此得到状态误差的线性递推关系:
$$
\delta x_k = F\delta x_{k-1}+Gn_{k-1}
$$
注意$F$是$f(x_{k-1},u_{k-1})$也就是状态量$x_k$对状态量$\hat x_{k-1}$的雅可比矩阵;G是状态量$x_k$对输入量$\hat u_{k-1}$的雅克比矩阵。(?在计算中经常采用状态量$x_k$对状态量$x_{k-1}$的雅克比矩阵近似?)
1.3.2、基于误差随时间变化的误差递推方程
如果能推导出状态误差随时间变化的导数关系,例如:
$$
\dot{\delta}x = A \delta x+Bn
$$
则误差状态的传递方程为:
$$
\delta x_k = \delta x_{k-1}+\dot{\delta}x_{k-1}\Delta t
$$
$$
\delta x_k = (\mathbf I+A \Delta t)\delta x_{k-1}+B \Delta t n_{k-1}
$$
由这两种方式可以看出:
$$
F=\mathbf I+A \Delta t,G=B \Delta t
$$
VINS-mono中的预积分残差传播公式便是使用这种方式表示的。
有了这个理论基础,我们便可以得出Algorithm 1中协方差矩阵的递推关系:

其中$F_t$矩阵是状态量$[p_{t+1},v_{k+1},\phi_{k+1},b_{ak+1},b_{gk+1}]$对状态量$[p_{t},v_{k},\phi_{k},b_{ak},b_{gk}]$的雅克比矩阵;$G_t$是状态量$[p_{t+1},v_{k+1},\phi_{k+1},b_{ak+1},b_{gk+1}]$对噪声项(也可当做输入量)$[\eta_k^a,\eta_k^g]$的雅可比矩阵。
当使用更精确的匀加速模型离散化积分公式(1.1),我们只需要在Algorithm 1算法的$p_{t+1}$项上加$\frac{1}{2}at^2$,这时协方差矩阵$F$有如下的形式:
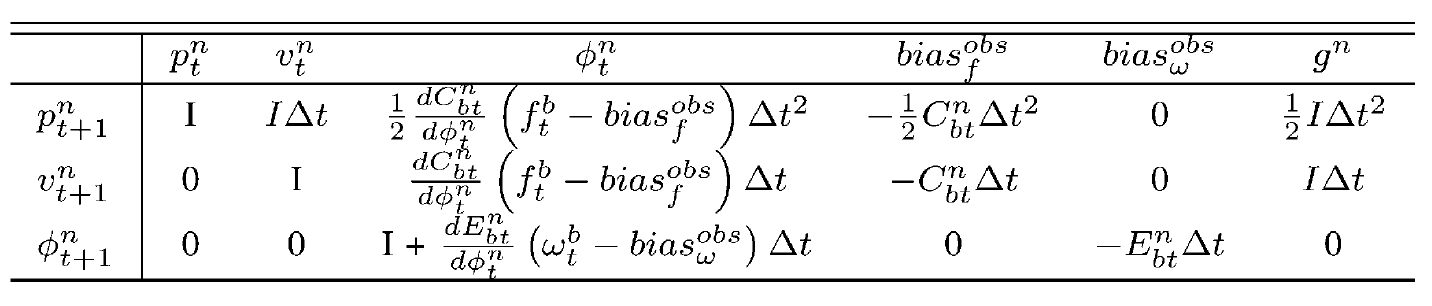
在Algorithm 1中,初始条件$[p_{t1}^n,v_{t1}^n,\phi_{t1}^n]$需要在算法初始时提供,加速度、角速度先被转换到导航坐标系下,之后再积分。从上表可以看出对初始条件的估计是一个非线性问题,非线性主要来自位姿的旋转项(旋转矩阵自身的约束关系,不同行、列满足正交关系、每行、列模长为1)以及IMU的bias。当使用线性的方法如EKF去估计初始条件就会导致解收敛缓慢或者不收敛。
文章的作者通过改变积分的参考坐标系,将对初值条件中的姿态估计转换为对重力的估计,进而将非线性问题转换为线性问题求解,接下来我们看看他是如何实现的?
2、预积分技术
2.1、 body系下的积分
不论使用何种初始化方法,对于Algorithm 1而言,IMU测量值都要在积分前先转换到导航坐标系下。和其他传感器相比,即使是低成本的IMU,采样频率也很高。这样在融合初始化时,需要对边缘化滤波器(marginalizing filter)(如EKF)进行高速率的更新,或者延迟状态方法需要大量的位姿状态。另一个问题,特别是对于批处理初始化的方法(batch initialized inertial methods),它需要存储大量的惯性观测,一旦初始条件可被观测,就需要在批滤波器中处理这些惯性观测。
如果在初始条件未知的情况下,这些观测值可以被整合在一起,那么大量的惯性观测值就可以被看作是滤波器中的一个单独的观测值,从而避免前面列出的问题。一个可行的方法是在载体坐标系下对IMU积分。对公式(1.1)重写,可以得到在载体系下的积分结果:
.png)
旋转矩阵$C_{bt}^{bt1}$在初始$t1$时刻$C_{bt1}^{bt1}$是单位矩阵。
与上一节在globallt frame中的积分不同,这些方程仍然需要全局参考坐标系下的载体初始位姿,但是各位姿之间的惯性观测值的积分是在第一个时刻$t_1$的载体坐标系中进行的,积分完成后再转化到导航坐标系下,而不是之前。将公式(2.1)中的积分项提取出来,我们称这些积分项为预积分项:
.png)
这些预积分项可以只根据IMU的测量值,在没有初始条件的情况下进行积分($\Delta p_{t2}^{+t1}$项再进行第二重积分时,初始速度可以当做是0,因为积分是在$t_1$时刻的body坐标系下完成的,相邻两时刻的IMU的相对瞬时速度可近似为0),表示了从姿态1到姿态2的位置、速度、旋转的变化(不严谨的说法)。它可以作为一个整体的观测来代替两帧(例如两个图像帧)之间所有IMU观测信息,这也是预积分名字的由来。将预积分项(2.2)重新带入公式(2.1)则有:
$$
\begin{array}{l}
p_{t2}^n=p_{t1}^n+(t_2-t_1)v_{t1}^n+\frac{1}{2}(t_2-t_1)^2g^n+C_{bt1}^n\Delta p_{t2}^{+t1} \\
v_{t2}^n=v_{t1}^n+(t_2-t_1)g^n+C_{bt1}^n\Delta v_{t2}^{t1} \\
\phi_{t2}^{n} = EulerFromDCM(C_{bt1}^n\Delta C_{bt2}^{bt1}) –旋转矩阵到欧拉角
\\
\end{array} \tag{2.3}
$$
$\Delta v_{t2}^{t1}$和$\Delta C_{bt2}^{bt1}$可直接代表两帧间速度与旋转的变化量,但是$\Delta p_{t2}^{+t1}$不能直接代表两帧之间位置的变化量,因为加速度计只提供加速度的测量,初始速度$v_{t1}^{n}$仍然是不可获取的。但是可以将$\Delta p^+$当做匀速运动模型的修正项,将加速度的影响考虑进来,”+”表示它不是真正意义上的变化量。
若使用运行运动模型,预积分的欧拉积分离散化为:

标准的惯性积分Algorithm 1算法需要载体的初始位置、速度和旋转,而预积分技术将所有的这些值设为0,便于积分。同时Algorithm 1算法的速度方程还需要考虑重力矢量,预积分则不需要考虑。
2.2、Bias修正
从Algorithm 3可以看出,IMU预积分不再需要初始速度和姿态,然而,IMU传感器的bias仍然存在于积分中。如果在预积分时存在bias的估计值,那么它们可以用来计算预积分,然而,如果bias不可用或者是不准确的,并在后端进行了优化,那么在不重新积分的情况下,能纠正这些偏差将是非常有用的。如果可以计算出公式(2.2)对bias的导数,那么这便是可行的,我们在$t_1$时刻对公式(2.2)泰勒展开:
$$
\begin{array}{l}
\Delta p_{t2}^{+t1} =\Delta p_{t2}^{+t1}+J_{b_{t1}^a}^\alpha \delta b_{t1}^a+J_{b_{t1}^g}^\alpha \delta b_{t1}^g
\\
\Delta v_{t2}^{t1} = \Delta v_{t2}^{t1} + J_{b_{t1}^a}^\beta \delta b_{t1}^a+J_{b_{t1}^g}^\beta \delta b_{t1}^g
\\
\Delta \phi_{t2}^{t1} = \Delta \phi_{t2}^{t1} + J_{b_{t1}^g}^ \phi \delta b_{t1}^g
\end{array} \tag{2.4}
$$
这些雅克比矩阵是下面J矩阵的对应子块:
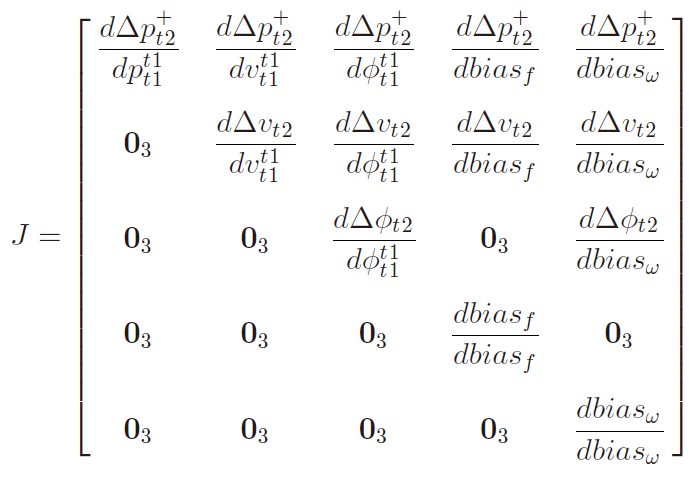
这些雅克比矩阵可以根据前面讨论的协方差传递公式,一步步递推得到:
$$
J_{t+1} = FJ_t \tag{2.5}
$$
与标准状态下的惯性积分相同,我们也需要获取预积分的不确定性,计算方法和1.3.1、基于一阶泰勒展开的误差递推方程中的计算方法一致,如下:
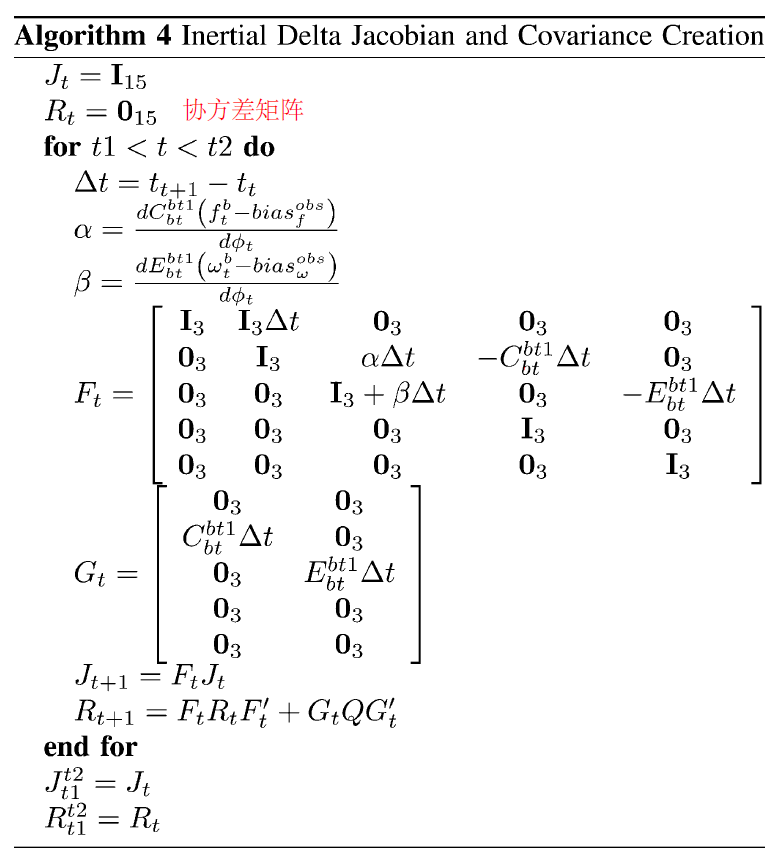
与标准惯性积分方差预测不同,这里主要是多了一个附加项,即观测不确定性的雅克比矩阵。
至此,预积分理论大部分已经介绍完成,VINS-Mono中的预积分与此相差无几,过几天会专门开一片文章推导VINS-mono中的基于中值积分的预积分。Todd Lupton在其2012年的文章中还推导了线性的视觉惯导联合初始化的方法,避免本篇文章过长,这一部分在下一篇文章中记录。
3、参考文献
1、Visual-Inertial-Aided Navigation for High-Dynamic Motion in Built Environments Without Initial Conditions
2、深蓝学院VIO课程——基于优化的IMU预积分与视觉信息融合
3、预积分公式总结与推导——邱笑晨

