反对称矩阵的性质
因为这一部分的知识比较少,本来打算将这块的内容插入到其他博客文章中。后来想想反对称矩阵在SLAM中特别常用,还是单独写一篇博客,详细地推导一些反对称矩阵的性质。
我们知道反对称矩阵的引入使得向量的叉乘可以写成如下的矩阵表示形式:
$$
\boldsymbol{a} \times \boldsymbol{b}=\left[\begin{array}{ccc}
\boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k} \\
a_{1} & a_{2} & a_{3} \\
b_{1} & b_{2} & b_{3}
\end{array}\right]=\left[\begin{array}{c}
a_{2} b_{3}-a_{3} b_{2} \\
a_{3} b_{1}-a_{1} b_{3} \\
a_{1} b_{2}-a_{2} b_{1}
\end{array}\right]=\left[\begin{array}{ccc}
0 & -a_{3} & a_{2} \\
a_{3} & 0 & -a_{1} \\
-a_{2} & a_{1} & 0
\end{array}\right] \boldsymbol{b} \triangleq \boldsymbol{a}^{\wedge} \boldsymbol{b}
$$
这个由一个三维向量表示的反对称矩阵有很多有用的性质,我们来开始推导。
(1)$\forall u,v \in R^3$,$v^{\wedge}u=-u^{\wedge}v$
这个结论没什么好说的,根据叉乘的性质这条显然成立。
(2)$v^{\wedge T} = -v^{\wedge}$
这一条也没什么好说的,根据反对称矩阵的表示形式显然成立。
(3)$v^{\wedge}u^{\wedge}=uv^T-v^TuI_{3\times 3}$
在证明这条性质之前我们先来看三重积公式:
$$
v\times (u\times a) = u(v\cdot a)-a(v\cdot u)
$$
相信很多人看这个公式觉得眼熟,但忘记是什么时候学的了,我也一样,这知识不用他就不进脑子。我们将这些个叉乘、点乘统统写成矩阵表示的形式,则有如下:
$$
v^{\wedge}u^{\wedge}a=uv^{T}a-av^{T}u
$$
注意到$v^{T}u$就是一个实数,所以我们可以将$a$提取出来:
$$
v^{\wedge}u^{\wedge}a=(uv^{T}-v^{T}uI_{3\times 3})a
$$
因为对于任意的$a\in R^{3}$上述公式都成立,所以我们就能得出:
$$
v^{\wedge}u^{\wedge}=uv^T-v^TuI_{3\times 3}
$$
所以第(3)条性质得以证明。
(4)$v^{\wedge 2} = vv^T-||v||^2_2 I_{3\times 3}$
这个性质是第(3)条性质的特例,这里的$||v||_2$表示向量$v$的二范数,等于向量$v$的模长$\sqrt{<v,v>}$。
(5)$v^{\wedge 3} = -||v||^{2}_{2}v^{ \wedge}$
在第(4)条性质的基础上我们左乘$v^{\wedge}$,因为$v\times v=0$所以我们很容易能得到这条性质。利用这条性质我们可以推导出来反对称矩阵$v^{\wedge}$的特征值,理解接来下的推导需要有一定的矩阵论基础。根据这个性质,我们可以写出$v^{\wedge}$的零化多项式,他就是$\lambda^3+||v||^2_2\lambda=0$,实际上这也是$v^{\wedge}$的最小多项式。那么最小多项式为什么不是$\lambda^2+||v||^2_2=0$呢?这是因为0是$v^{\wedge}$的一个特征值。
因为$v^{\wedge}v=0v$所以我们可以看出$v^{\wedge}$的核空间是一维的,0必定是$v^{\wedge}$的一个特征值,进而$v^{\wedge}$一定是不满秩的,$v^{\wedge}$不可逆!(所以我们想在第(5)条性质的左右两端乘以$v^{\wedge}$的逆来降低零化多项式的维度是不可取的)。我们解$v^{\wedge}$的最小多项式,可以得到$v^{\wedge}$的三个特征值如下:
$$
\lambda_1=0、\lambda_{2,3}=i||v||_2
$$
(6)$rank(v^{\wedge})=2,v \neq0$
在第(5)条性质中,我们求解出了$v^{\wedge}$的特征值,有一个是0,另外两个是相等的虚数,所以在$v\neq0$的情况下,$v^{\wedge}$的秩一定是2。当$v=0$时,$v^{\wedge}$是一个零矩阵,零矩阵的秩自然为0了。
(7)$Null(v^{\wedge})=span(v) $
在第(5)条性质的推导中,显然能看到这个结论成立。
(8)$a,b,c \in R^{3},a^Tb^{\wedge}c=b^Tc^{\wedge}a=c^Ta^{\wedge}b$——轮换对称性
这条性质是与混合积的性质等价的:$a\cdot (b\times c)=b\cdot (c\times a)=c\cdot(a\times b)$。混合积是有几何和代数意义的:
- 几何意义:表示以$a,b,c$为棱长组成的平行6面体的体积;
- 代数意义:$det([a,b,c])=a\cdot(b\times c)$;轮换对称性正是因为偶数次的列交换不改变矩阵的行列式。
(9) $a=Ub,\quad a,b\in R^3,\quad U\in R^{3\times 3},\quad |U|=1$(右手系),$U^TU=$(正交系),则有$a^{\wedge}=(Ub)^{\wedge}=Ub^{\wedge}U^T$。
这条性质属于反对称矩阵的变换性质,在SLAM中我们经常使用旋转矩阵对点进行变换,这条性质会被经常用到。证明如下:
$$
(Ub)^{\wedge} = Ub^{\wedge}U^T \\
$$
$$
\begin{aligned}
&\Leftrightarrow (Ub)^{\wedge}U=Ub^{\wedge}U^TU=Ub^{\wedge} \\
&\Leftrightarrow \forall a \in R^3, \quad (Ub)^{\wedge}Ua=Ub^{\wedge}a \\
&\Leftrightarrow \forall a \in R^3, \quad (Ub)\times(Ua) = U(b\times a)
\end{aligned}
$$
最后一个公式利用向量叉乘的旋转变换不变性可以证明,之后我们可以反推出来本条性质的正确性。
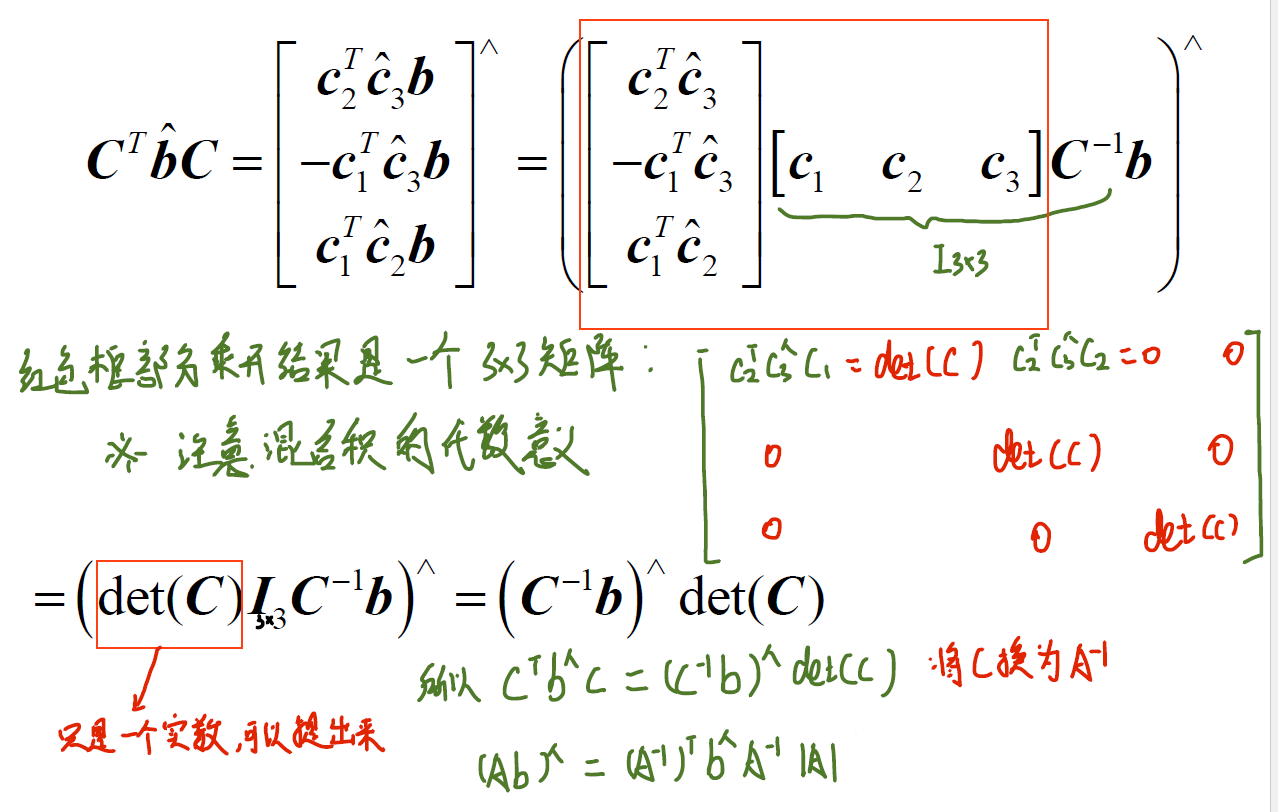
(10)$a=Ab,\quad a,b\in R^3,\quad A \in R^{3\times 3},\quad |A| \neq0$,则有$a^{\wedge}=(A^{-1})^Tb^{\wedge}A^{-1}\cdot|A|$。
可以看出第(9)条性质不过是这条性质的一个特例,它不要求变换是右手系的旋转矩阵,但变换要满足可逆条件,一个证明如下: