单目视觉惯导在线初始化——时空校准
该方法可以在线标定相机与IMU之间的相对位姿(空间)和时间(时间)偏移以及估计初始阶段的尺度、速度、重力、陀螺仪和加速度计Bias的初始值。看该方法前,请务必了解预积分的相关知识,可以看之前我写的几篇博客。
该算法分为三个步骤:
- 通过最小化相机和IMU之间的旋转误差来估计外参中的旋转、时间偏移(time offset)和陀螺仪Bias;
- 利用插值得到的摄像机位姿,忽略加速度计的Bias,近似估计尺度因子、重力矢量和外参中的平移向量;
- 通过考虑加速度计偏差和重力大小,在第二种过程中估计的值进一步细化。
1、传感器短时运动插值
首先对时间偏移量建模:
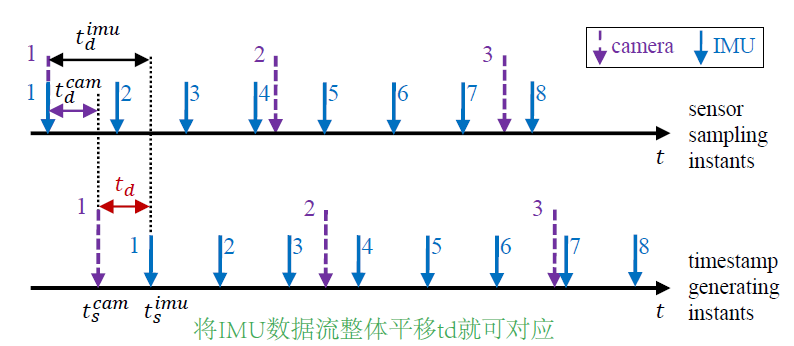
如上图所示,每个传感器以恒定频率离散采样(上面的坐标轴),然而,由于时钟不同步、传输延迟、传感器响应和操作系统开销等,总是存在一个延迟,使测量流(时间戳生成流,下面的坐标轴)与采样流不一致。考虑IMU和相机在同一时刻采样,对于每一个传感器,其时间戳$t_s$与真实的采样时间$t$存在一个延迟$t_d$:
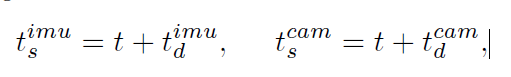
不同传感器的时间延迟一般是不一样的,这就导致上图中的现象,实际第1帧与第2帧图像帧之间有第1、2、3、4帧IMU的测量数据(采样流),但是由于相机和IMU的延迟不同,从测量流中读取到的数据就会变为第1帧与第2帧图像帧之间有只有第1、2、3帧的IMU测量数据,这就会导致IMU预积分的不准确。所以估计不同传感器时间延迟之间的差值$t_d$是有必要的。

这样通过将Camera的测量流滞后$t_d$或者将IMU的测量流提前$t_d$就可将两个传感器对齐,如此便有下面的关系:
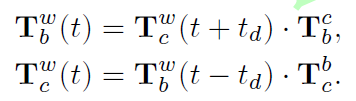
这里,$T_{b}^w(t)$和$T_{c}^w(t)$分别是IMU和相机在时间戳$t$处的位姿。
下面使用线性插值方法获得$T(t+t_d)$的近似计算,假设相机在短时间内的运动是匀速的,则任意时刻的相机位姿可以用其最近的相机位姿、角速度和线速度插值获得。若$T_{c_i}^{w}$与$T_{c_j}^{w}$是单目VO获得的在时间戳$t_{c_i}$和$t_{c_j}$处的位姿,则相机在时间戳$t_{c_i}$的角速度$\omega_{c_i}$和线速度$\tilde v_{c_i}$可通过下式获取:(注意,速度与米制单位相差一个尺度$s$)

相机在$t_i+t_d$处的位姿通过线性插值得到:

同理IMU在$t_i-t_d$处的位姿也可通过线性插值得到:

这里的$\overline \omega_{b_i}$是$t_i$时刻IMU坐标系下的角速度,$v_{b_i}^w$是IMU的线速度在世界坐标系下的表示。
2、转换关系
考虑time offset $t_d$和尺度因子$s$,根据IMU与相机时间对齐的关系(上边的公式),在时间戳$t_i$处IMU系的旋转和平移可分别表示为:

3、三步走初始化策略
3.1、外参中的旋转、时间偏移(time offset)和陀螺仪Bias修正
直接引入预积分的公式,这个公式来自VINS-Mono中的推导,$\alpha_{b_{k+1}}^{b_k}$、$\beta_{b_{k+1}}^{b_k}$、$\gamma_{b_{k+1}}^{b_k}$就是预积分的位置项、速度项、旋转项(四元数表示):
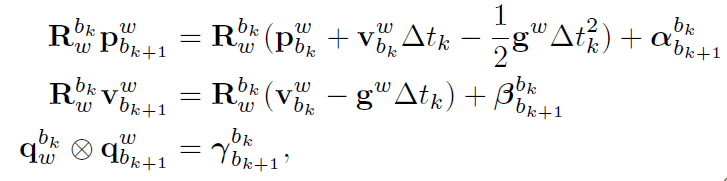
预积分项的线性修正(bias修正,详情请看IMU预积分系列文章):
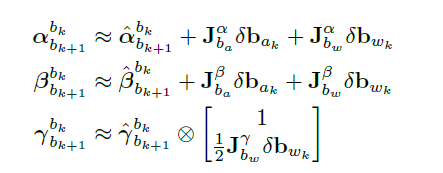
于是IMU预积分旋转项的误差为:
$$ e_{rot(k,k+1)}= \left[(\hat{\gamma}_{b_{k+1}}^{b_{k}} \otimes\left[\begin{array}{c} 1 \\\\ \frac{1}{2} \mathbf{J}_{b_{w}}^{\gamma} \delta \mathbf{b}_{w_{k}} \end{array}\right])^{-1}q_{w}^{b_k}\otimes q_{b_{k+1}}^{w}\right]_{x y z} $$根据第二节2、转换关系的公式,可有:
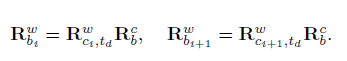
考虑time offset,重新带入$e_{rot(k,k+1)}$中,则有:

这里使用旋转矩阵代替了四元数的表示方法,本质上都是一样的。若有N帧关键帧,外参中的旋转$R_b^c$、time offset $t_d$、陀螺仪的bias $\delta b_g$可以通过最小化所有帧的旋转项误差来获得:
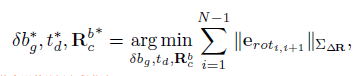
这里使用加权的最小二乘,$\sum _{\Delta R}$是预积分旋转项的信息矩阵。这个信息矩阵可从IMU预积分时的协方差矩阵中提取。在恢复出陀螺仪的Bias后,根据新的陀螺仪Bias重新计算预积分,获取更加精确的预积分结果。
3.2、近似的尺度、重力和外参中的平移项修正
一旦外参的旋转$R_c^b$、time offset $t_d$、陀螺仪的bias $\delta_{b_g}$估计出来,尺度因子$s$、重力矢量$g^w$和外参中的平移$p_b^c$就可粗略的估计了。预积分中的位移项和速度项可以写为:
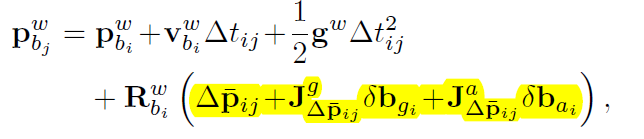
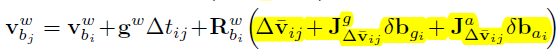
这个步骤不估计加速度计的bias,令$J_{\Delta \overline p_{ij}}^{a}$与$J_{\Delta \overline v_{ij}}^{a}$为0,同样在估计出陀螺仪的bias后,重新计算预积分,这里的$J_{\Delta \overline p_{ij}}^{g}$与$J_{\Delta \overline v_{ij}}^{g}$同样设为0。
将第2节转换关系中的公式带入,可有:

其中$R_b^{c*}$是第一步估计出的结果,考虑连续的三帧$i,i+1,i+2$和速度预积分项,将上式中的$v_{bi}^w$搞掉,并将待估计变量$s$、$g^w$、$p_b^c$分离出来,写成矩阵表示的形式,有:

其中:
若有$N$帧,可以获得$N-2$个上述的约束方程,所有的观测可以堆叠成一个线性超定方程$B_{3(N-2) \times 7} \cdot X_{7 \times 1} = C_{3(N-2) \times 1}$。可见至少5帧才可求解,求解这个方程可使用SVD分解。得到的粗略估计结果记为$s^*$,$g^{w*}$,$P_b^{c*}$。
3.3、估计加速度计偏置,Refine尺度、重力、外参中的平移矢量
在这一步,将地球坐标系下的重力矢量的模长考虑进来,进而refine尺度、重力、外参中的平移矢量。使用上一步估计出来的重力矢量$g^{w*}$,将这个矢量与地球坐标下的重力矢量$G^e$的方向对齐:

通过加入一个微小的扰动对旋转矩阵$R_e^w$进行调整:
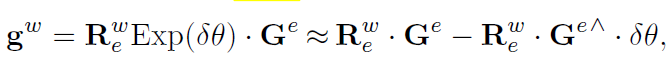
将重新参数化的重力带入3.2节中的公式,可有:

在这一步中估计加速度计的bias,相关的Jacobian矩阵不当做0来处理了,同样的手段,考虑连续的三帧、搞掉速度项并写成矩阵表示的形式,可有:

其中:

$[ \cdot ](:,1:2)$表示矩阵的前两列。若有$N$帧,可以获得$N-2$个上述的约束方程,所有的观测可以堆叠成一个线性超定方程$D_{3(N-2) \times 9} \cdot y_{9 \times 1} = E_{3(N-2) \times 1}$。注意上面的$\delta \theta_{xy}$表示只估计roll和pitch角,因为yaw角不可观测。
上述变量估计出来后,加速度计的bias为:$b_a = 0_{3 \times 1}+\delta b_a$,优化后的重力矢量为:$g^{w} = R_e^wExp(\delta \theta)G^e$。
4、初始速度估计
重力矢量估计出来后,速度项的估计就是水到渠成的事情了,根据预积分的平移项,可有
$$
v_{b_i}^w = \frac{p_{bj}^{w}-p_{bi}^{w}-\frac{1}{2}g^w\Delta t_{ij}^2-R_{bi}^w \Delta \overline p_{ij}}{\Delta t_{ij}}
$$
5、附录:3.1节非线性优化所需的Jacobian的推导
6、参考文献
1、Visual-Inertial-Aided Navigation for High-Dynamic Motion in Built Environments Without Initial Conditions
2、Online Initialization and Extrinsic Spatial-Temporal Calibration for Monocular Visual-Inertial Odometry

