GWH Blog

LeGo-LOAM中的featureAssociation节点

发表于 分类于 ， ，
本文字数： 15k 阅读时长 ≈ 13 分钟

LeGo-LOAM中的featureAssociation节点

LeGo-LOAM是在LOAM基础上改进的激光雷达定位与建图方法，它对地面点进行了优化、提出了两步LM优化算法，加入了闭环检测和全局因子图优化等。
本系列博客只说明了关键代码的功能实现，以及一些关键地方的数学推导，详细的解释都写在了代码注释中，注释后的代码在融合相机后会传到github。同时也列出来一些问题提醒自己有条件时实际去验证。

这个模块接收四种消息：

  • 从”/segmented_cloud”话题接收到的分割点云（1/5地面点和有效分割点），保存到成员变量segmentedCloud中；
  • 从”/segmented_cloud_info”话题接收到的描述segmentedCloud点云的附加信息，保存到成员变量segInfo中；
  • 从”/outlier_cloud”话题接收到的外点（5倍降采样后的非地面无效分割点云），保存到outlierCloud中；
  • 从”/imu/data”话题接收原始IMU数据，将数据存入缓存队列，并进行惯性积分；

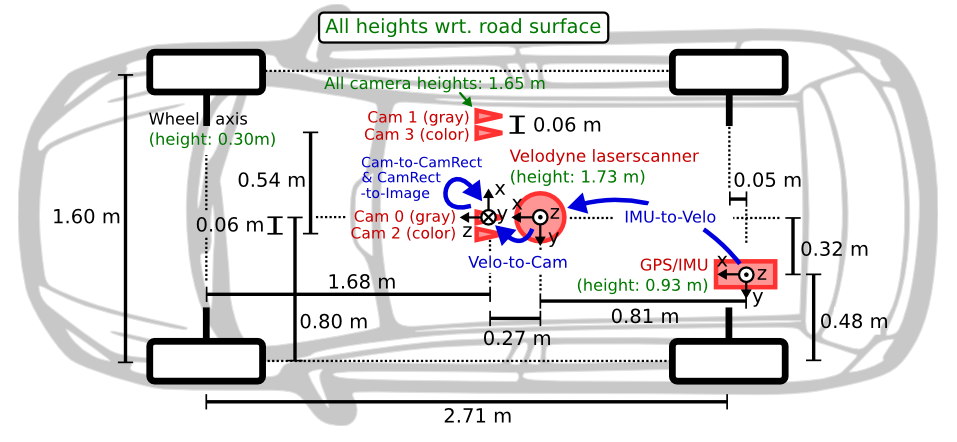
Lego-LOAM可选择使用高频的IMU来辅助进行运动补偿，去除点云的畸变。辅助去除运动中的非线性项，使得帧间运动符合匀速运动假设是IMU最大的作用，IMU并未用来紧耦合或者松耦合位姿。IMU的处理在featureAssociation.cpp中，从代码中来看，Lego-LOAM要求IMU能够提供方位角orientation、加速度linear_acceleration、角速度angular_velocity，且IMU的频率至少是要高于Lidar的频率的。这个cpp文件中隐含了传感器间的坐标关系，它与KITTI数据集中IMU与Lidar的坐标关系保持一致：

featureAssociation.cpp中有两个重要的接口函数，其中一个就是FeatureAssociation的构造函数，重点在它定义了接收消息的回调函数：

1
2
3
4
5
6
7
8
9
10
11
FeatureAssociation() : nh("~") {
  // 地面点(仅有1/5)和有效分割点，intensity通道为对应点在rangeMat_中的索引
  subLaserCloud = nh.subscribe<sensor_msgs::PointCloud2>("/segmented_cloud", 1, &FeatureAssociation::laserCloudHandler, this);
  // 接收imageProjection.cpp中的segMsg_
  subLaserCloudInfo = nh.subscribe<cloud_msgs::cloud_info>("/segmented_cloud_info", 1, &FeatureAssociation::laserCloudInfoHandler, this);
  // 非地面无效分割点云(5倍降采样后)，intensity通道表示对应点在rangeMat_中的索引
  subOutlierCloud = nh.subscribe<sensor_msgs::PointCloud2>("/outlier_cloud", 1, &FeatureAssociation::outlierCloudHandler, this);
  // 接收IMU的消息，IMU频率比较高，所以缓存区设的比较大
  subImu = nh.subscribe<sensor_msgs::Imu>(imuTopic, 50, &FeatureAssociation::imuHandler, this);
 ...
}

除了IMU消息的回调函数，其他消息的回调函数功能都比较单一，就是简单的将接收到的消息转存到对应的成员变量中。

1、回调函数imuHandler()中完成的处理

我们必须明确IMU的原始测量值是相对于惯性空间的测量在载体坐标系(body系)下的投影！IMU数据通过imuHandler()函数读入，每来一帧IMU数据，首先要完成以下几件事情：

  1. 根据方位角信息去除重力对加速度的影响，计算得到IMU的真实加速度（body系下）；
  2. 进行坐标轴交换，统一到z轴向前,x轴向左，y轴向上的右手坐标系；
  3. 将当前帧IMU消息的时间戳、方位角、真实加速度(body系下)、角速度（body系下），保存到imuTime[]，imuRoll、Pitch、Yaw[]，imuAccX、Y、Z[]，imuAngularVeloX、Y、Z[]缓存队列中；
  4. 调用函数AccumulateIMUShiftAndRotation()进行速度、位移、角度积分。

2、AccumulateIMUShiftAndRotation()函数完成惯性积分：

  1. 缓存队列中存储的IMU测量值是在body系下的投影，这里计算速度积分、位置积分时先把加速度投影到惯性系下；
  2. 只有当IMU的频率高于Lidar的频率，才进行惯性积分，惯性积分得到当前IMU帧在惯性系下的速度、惯性系下的位移、以及相对于首帧IMU的旋转；这三种信息分别保存在队列imuVeloX、Y、Z[]，imuShiftX、Y、Z[]，imuAngularRotationX、Y、Z[]中；

这里需要注意的是原始IMU消息所在的坐标系是x轴向前，y轴向左，z轴向上的右手坐标系，Lego-LOAM对坐标系进行了统一，统一转换到z轴向前，x轴向左，y轴向上的右手坐标系。在imuHandler()函数中，只对加速度做了这个转换，方位角、角速度还在原来x轴向前的坐标系下。所以这里在后续计算的时候需要注意，例如我们从一帧IMU消息中读取到方位角orientation，根据这个方位角计算出来roll、pitch、yaw，则$Rz(yaw)Ry(pitch)Rx(roll)$表示的是原始IMU坐标系到惯性系的旋转变换，表示为$R_{xyz}^{w}$；那么新的IMU坐标系到惯性系的旋转变换$R_{zxy}^{w}$是这样计算的：$Ry(yaw)Rx(pitch)Rz(roll)$。

另外一个接口函数是在接收到消息后才被使用的，它是runFeatureAssociation()——FeatureAssociation节点真正处理数据的函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
  void runFeatureAssociation()
  {
    // 判断如果3个点云消息都接收成功，且时间戳一致，才开始执行程序
	...
    // 主要对激光点统一坐标系，计算激光点在一帧中的时间比例s，若有IMU，去除点云旋转畸变以及加减速产生的畸变（之后可使用匀速模型补偿位移畸变）
    adjustDistortion();
    // 对segmentedCloud中所有点计算曲率，并保存曲率的计算结果
    calculateSmoothness();
    // LOAM论文中在提取激光特征点时说明了两种不稳定的情况，这个函数就是处理这的
    markOccludedPoints();
    // 提取特征点，这一步减少了参与后续计算的点云中点的数量，减少了计算量
    extractFeatures();
    // 发布当前帧提取的sharp、lessSharp、flat和lessFlat特征点集
    publishCloud();

    // 如果系统还未初始化
    if (!systemInitedLM)
    {
      // 跳过第一帧点云，关键在于将第一帧的点云设为source点云
      checkSystemInitialization();
      return;
    }

    // 给待估计变量transformCur[]赋一个初始值
    updateInitialGuess();
    // 构建距离约束，求解帧间位姿transformCur[]
    updateTransformation();
    // 帧间位姿transformCur[]整合为全局位姿transformSum[]
    integrateTransformation();

    publishOdometry();
	// cloud to mapOptimization
    publishCloudsLast(); 
  }
};

IMU的作用主要体现在adjustDistortion()函数中，若不使用IMU，这个函数的功能很简单，可以参考A-LOAM的代码。下面我会说明使用IMU和不使用IMU的差别体现在哪里。以下是我对代码的理解，不保证完全正确。

左边这幅图来自LOAM的原论文，它清楚的说明了如何estimate lidar motion。稍微解释一下，$t_k$表示第一帧点云的采样时刻，$t_{k+1}$表示第二帧点云的采样时刻，若Lidar的采样频率是10Hz，那么$t_{k+1} - t_{k} = 100ms$。蓝色的线表示这100ms内一帧点云中点的数量是线性增长的，绿色的线表示将一帧点云去畸变后投影到当前帧结束点时刻的Lidar坐标系下。同时这幅图默认第一帧点云结束点时刻等于第二帧点云起始点时刻，若按LOAM中的硬件（使用单线雷达来模拟3D雷达）能较好的符合这种假设，使用3D雷达可不会是这种情况，大部分会是右边的图描述的情况。使用右边的图来解释代码中IMU的部分会更好理解。

3、运动补偿函数adjustDistortion()中完成的处理

1、若不使用IMU，这个函数就是计算一帧segmented_cloud点云中每一点的时间比例因子s，并存储起来给后续函数使用：
$$
s = \frac{t_i - t_{start}}{scanPeriod}
$$
2、若使用IMU，除了第1步，这里还会去除点云加减速产生的位移畸变以及旋转畸变：

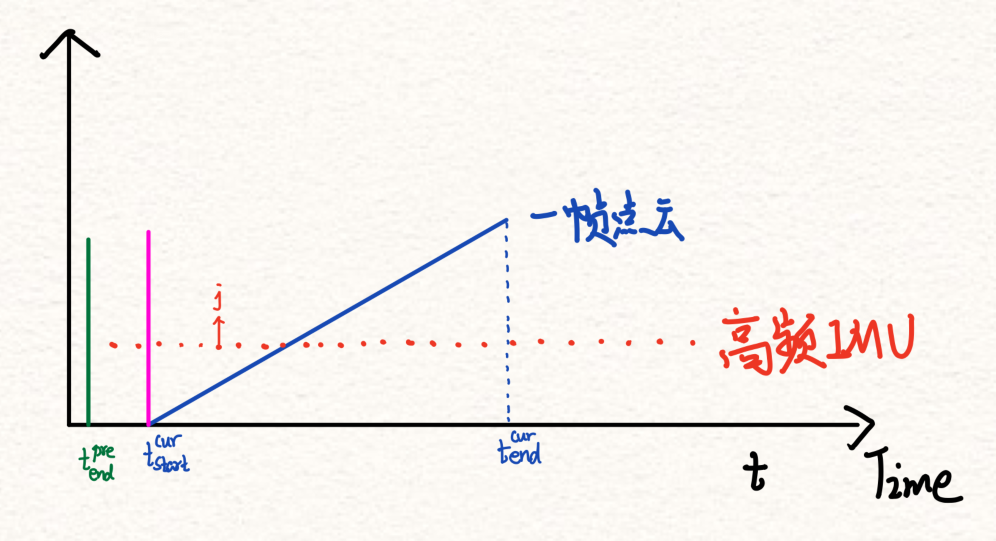
对于点云中的激光点，首先在时间轴上找到其左右两侧最近的IMU数据，进行一个线性插值来近似该时刻Lidar坐标系在惯性系下的方位角、速度以及位移。根据第j个激光点时刻lidar坐标系的方位角，可以计算此时Lidar系到惯性系的旋转变换$R_{lidar_j}^{n}$。由此可将一帧点云的旋转部分的畸变去除，即对应上图中粉色的线，旋转部分去掉畸变投影到起始点时刻Lidar坐标系下：
$$
P^{lidar_{start}} = (R_{lidar_{start}}^{n})^{-1} R_{lidar_j}^{n} P^{lidar_j}
$$
根据第j个激光点时刻lidar坐标系在惯性系下的位移，以及第0个激光点时刻lidar坐标系在惯性系下的位移和速度，可以计算由于加减速产生的位移：
$$
\Delta p = P_j^{n} - P_{0}^{n} - V_{0}^{n} \times \Delta t
$$
这个位移是在惯性坐标系下的，将这个位移根据第0个激光点时刻lidar坐标系的方位角，转换到第0个激光点时刻lidar坐标系下：
$$
\Delta p_{lidar_j}^{lidar_{start}} = R_{n}^{lidar_{start}} \Delta p
$$
如此去除非线性运动造成的点云畸变。经过这步处理，一帧点云可以看做投影到了起始点时刻Lidar坐标系下（旋转部分），位移部分从此符合匀速运动假设。

时间戳的说明：可以看出来若不使用IMU，点云的时间戳在一帧点云的起始、中间、结束时刻都不要紧，因为这里只计算时间比例因子供给后续函数使用，它与时间戳无关！但是使用IMU后，若还想保持原有点云的去畸变方式，就需要知道点云的起始时刻以及一帧点云的采样时间（用来寻找时间范围内的IMU数据），若点云的时间戳在一帧点云的中间，如KITTI数据集，就得根据这个时间戳近似一个起始时刻的时间戳来使用。（PS：KITTI数据集的IMU频率与雷达频率一致，不做额外努力也用不了IMU）。

4、计算曲率、提取特征点

calculateSmoothness()函数计算点云segmentedCloud中每个点的曲率，这里曲率的计算与LOAM中的不同，Lego-LOAM中第i个点的曲率按照如下公式计算：
$$
\begin{aligned}
&d_i = sqrt(x_i^2+y_i^2+z_i^2)\\
&diffRange_i = d_{i-5}+d_{i-4}+d_{i-3}+d_{i-2}+d_{i-1}+d_{i+1}+d_{i+2}+d_{i+3}+d_{i+4}+d_{i+5}-10d_{i}\\
&Curvature_i = diffRange_i * diffRange_i
\end{aligned}
$$
markOccludedPoints()函数对不可靠的点进行去除，不可靠的点就是LOAM论文中提及的（a）激光点平行于激光线、（b）遮挡区域后方的点这两种情况。

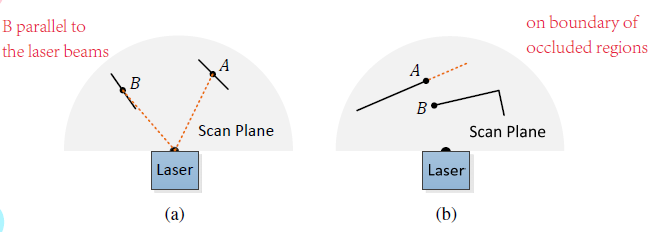
判断的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
 * @brief    遍历segmentedCloud，剔除不可靠点
 * 
 * 1、对LOAM中出现遮挡、障碍物平行于激光线扫的情况进行处理，LOAM中的Fig.4的(b)、(a)两种情况
 * 2、将不稳定点的cloudNeighborPicked[]标记为1，不会在这些点上提取特征点
 */
void markOccludedPoints()  {
  int cloudSize = segmentedCloud->points.size();
  for (int i = 5; i < cloudSize - 6; ++i) {
    float depth1 = segInfo.segmentedCloudRange[i];
    float depth2 = segInfo.segmentedCloudRange[i + 1];
    int columnDiff = std::abs(int(segInfo.segmentedCloudColInd[i + 1] - segInfo.segmentedCloudColInd[i]));
    // 如果这两点水平线束差小于10 (Horizon_SCAN)
    // 点云之间相互遮挡，而且又靠得很近的点，LOAM论文Fig.4的(b)情况
    if (columnDiff < 10) {
      // 将位于远处的5个点标记为1，这些点不会被选为特征点（Velodyne雷达顺时针扫描）
      if (depth1 - depth2 > 0.3) {
        cloudNeighborPicked[i - 5] = 1;
        cloudNeighborPicked[i - 4] = 1;
        cloudNeighborPicked[i - 3] = 1;
        cloudNeighborPicked[i - 2] = 1;
        cloudNeighborPicked[i - 1] = 1;
        cloudNeighborPicked[i] = 1;
      }
      else if (depth2 - depth1 > 0.3){
        cloudNeighborPicked[i + 1] = 1;
        cloudNeighborPicked[i + 2] = 1;
        cloudNeighborPicked[i + 3] = 1;
        cloudNeighborPicked[i + 4] = 1;
        cloudNeighborPicked[i + 5] = 1;
        cloudNeighborPicked[i + 6] = 1;
      }
    }
    // 障碍物平行于laser beam，LOAM论文Fig.4的(a)情况
    float diff1 = std::abs(segInfo.segmentedCloudRange[i - 1] - segInfo.segmentedCloudRange[i]);
    float diff2 = std::abs(segInfo.segmentedCloudRange[i + 1] - segInfo.segmentedCloudRange[i]);
    if (diff1 > 0.02 * segInfo.segmentedCloudRange[i] && diff2 > 0.02 * segInfo.segmentedCloudRange[i])
      cloudNeighborPicked[i] = 1;
  }
}

extractFeatures()函数用来提取特征点，Lego-LOAM自称是Ground-Optimized，在这个函数里就可以体现。遍历一帧点云中的每条scan，为了使特征点均匀分布，将一条scan分成6片。每片扇区在非地面分割点上选取2个曲率最大的点作为极大边线点集，在非地面分割点上选取20个曲率最大点作为次极大边线点集；每片扇区在地面点上选取4个曲率最小的点作为极小平面点集，除去次极大边线点集后剩余的点作为次极小平面点集。这个次极小平面点集比较大，进行了一次降采样。

5、checkSystemInitialization()初始系统

此函数主要用来跳过第一帧点云，将第一帧点云设为source点云，同时还有一个小细节：

1
2
3
4
5
// 从IMU消息中保存初始帧在惯性系下的Roll和Pitch角，作为累积位姿的初始值
// Yaw角和pos部分都未赋初值，即假设开始时刻的偏航角为0，位于惯性系下的原点位置，静态地球假设下，东北天坐标系当做惯性系
// 这里可以理解为IMU的加入使得系统的roll和pitch角可观，若使用IMU，则world坐标系就是第一帧点云处的东北天
transformSum[0] += imuPitchStart;
transformSum[2] += imuRollStart;

6、updateInitialGuess()给优化变量赋予初始值

transformCur[]是本模块的待优化变量，在这个函数中给他赋予初始值。transformCur[0~2]是欧拉角、tansformCur[3~5]是平移项，是否加入IMU，在给transformCur[0~2]赋予初始值时应该体现出来：

若使用IMU，旋转项transformCur[0~2]应该表示粉色的点云到绿色点云的位姿变换，它是一个小量，旋转项对应的欧拉角直接赋值为0比较好；若不使用IMU，点云的旋转畸变没有得到补偿，旋转项transformCur[0~2]表示的是当前帧最后一点到当前帧点云初始点的位姿变换$R_{end}^{start}$，实际应该是当前帧结束点到上一帧点云结束点的位姿变换，有差别，但是不大，置于为什么是这样，稍后在函数integrateTransformation()中说明，原始代码中旋转项transformCur[0~2]赋予的初始值为：

1
2
3
4
5
6
7
8
9
// 使用上一帧点云转过的角度给当前帧点云转过的角度赋一个初始值，即给transformCur中的旋转项赋一个初始值
// transformCur[]要表示的是当前帧最后一点到当前帧点云初始点的位姿变换T_{end}^{start}
// 此时R_{end}^{start} = Ry(-yaw)*Rx(-pitch)*Rz(-roll)
if (imuAngularFromStartX != 0 || imuAngularFromStartY != 0 || imuAngularFromStartZ != 0){
	transformCur[0] = - imuAngularFromStartY;  // = pitch
	transformCur[1] = - imuAngularFromStartZ;  // = yaw        
	transformCur[2] = - imuAngularFromStartX;  // = roll
    // TODO::若没有去除旋转项的畸变这样赋初始值比较好，若点云旋转的畸变去除了，赋0比较好
}

代码中的roll、pitch、yaw还是在原始x轴向前，y轴向左，z轴向上的IMU系下，注意这里有一个负号，所以TransformToStart()函数对应的变换是这个if语句上面注释的旋转变换。

transformCur[3~5]是平移项，平移项和旋转项表示的含义不相同，平移表示当前帧起始点到当前帧点云结束点的位置变换，实际应该是上一帧结束点到当前帧点云结束点的位置变换，$t_{start}^{end}$，原始代码中平移项transformCur[3~5]赋予的初始值为：

1
2
3
4
5
6
7
8
9
10
11
12
// 根据速度畸变，为transformCur的平移项赋一个初始值，(对于匀速运动假设的一个补偿)
// imuVeloFromStartX表示的是start系下的速度，乘时间表示的是t_{end}^{start}
// 但是这里没有直接赋值，而是都取了一个负数，这样transformCur[]要表达的就不是我们想要的含义了，它是t_{start}^{end}不是t_{end}^{start}
// **************************************************************************************
// 全篇代码并没用用到IMU与Lidar之间的外参，IMU测量得到的角速度、加速度并没用先转换到lidar坐标系下
// 这里的代码说明，只是使用IMU系的近似旋转、速度来给lidar帧的旋转、位移赋一个初始值而已，可以不太精细
// **************************************************************************************
if (imuVeloFromStartX != 0 || imuVeloFromStartY != 0 || imuVeloFromStartZ != 0){
	transformCur[3] -= imuVeloFromStartX * scanPeriod;
	transformCur[4] -= imuVeloFromStartY * scanPeriod;   // TODO:: 这里初值赋予的也不是那回事
	transformCur[5] -= imuVeloFromStartZ * scanPeriod;
}

7、updateTransformation()构建距离约束，求解帧间位姿

这个函数里使用LOAM中的方法构建约束关系，并求解。此函数分为两部分，一是在次极大边线点集中寻找极大边线点的匹配线，建立点到直线的距离约束；在次极小平面点集中寻找极小平面点的匹配面，建立点到平面的距离约束。二是使用Gauss-Newton优化算法迭代求解（论文中说用的LM算法，代码中并不是）。Lego-LOAM提出来two-step L-M优化算法，第一步，根据平面点的约束求解[t_z, roll, pitch]，对应函数calculateTransformationSurf()，第二步，根据边线点的约束求解[t_x, t_y, yaw]，对应函数calculateTransformationCorner()。

按照LOAM中的方法，在建立距离约束的过程中，点云会被投影到一帧的开始点时刻，即对应TransformToStart()函数，在不使用IMU的时候，原始代码是没有问题的，这个函数完成的功能如下：
$$
\begin{aligned}
p^{start} &= R_{cur}^{start}p^{cur} + t_{cur}^{start} \\
&= R_{cur}^{start}p^{cur} - R_{cur}^{start}t_{start}^{cur} \\
&= R_{cur}^{start}(p^{cur} - t_{start}^{cur})
\end{aligned}
$$

其中:

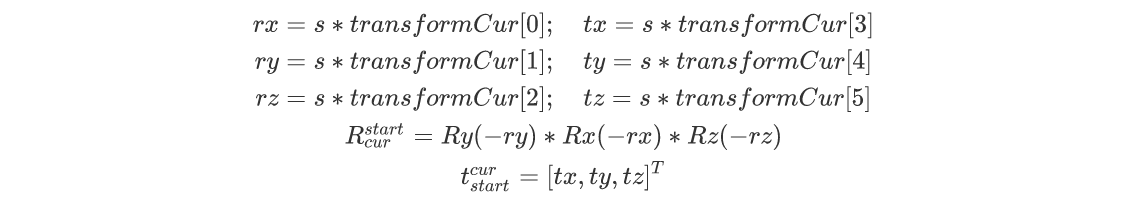
但是使用IMU时，这里出现了问题！在adjustDistortion()函数调用TransformToStartIMU()函数时，点云的旋转畸变已经去掉了，transformCur[]的含义已经发生了改变，原始代码中这样处理不是很合理。推导如下：去畸变的过程就是将100ms内采集到的激光点都统一到某一时刻，LOAM以及LeGo-LOAM都统一到一帧点云起始点时刻的Lidar坐标系下，对应的公式是：
$$
\begin{aligned}
P^{start} &= T_{cur}^{start}P^{cur} \\
&=(T_{start}^{n})^{-1}T_{cur}^{n}P^{cur} \\
&=
\left[
\begin{array}{cc}
R_{start}^{n} & t_{start}^{n} \\
0 & 1
\end{array}
\right]^{-1}
\left[
\begin{array}{cc}
R_{cur}^{n} & t_{cur}^{n} \\
0 & 1
\end{array}
\right]
P^{cur} \\
&=(R_{start}^{n})^{-1}R_{cur}^{n}P^{cur}+(R_{start}^{n})^{-1}(t_{cur}^{n} - t_{start}^{n})
\end{aligned}
$$
推导过程中隐含了一次齐次坐标到非齐次坐标的转换，这个公式的前半部分在adjustDistortion()函数中已经实现，只差后半部分。后半部分表示的就是$t_{cur}^{start}$，即transformCur[3~5]的相反数。所以使用IMU后，这个函数这样写就可以了：

1
2
3
4
5
6
7
8
9
10
11
12
void TransformToStart(PointType const *const pi, PointType *const po) {
  // 这里乘10，相当于除以scanPeriod = 0.1
  // TODO::这里不精确，segInfo中已经包括了当前帧点云初始点与结束点之间的角度差值
  float s = 10 * (pi->intensity - int(pi->intensity));
  float tx = s * transformCur[3];
  float ty = s * transformCur[4];
  float tz = s * transformCur[5];
  po->x = pi->x - tx;
  po->y = pi->y - ty;
  po->z = pi->z - tz;
  po->intensity = pi->intensity;
}

在原始代码中，使用IMU去掉旋转畸变后，transformCur[0~2]就是一个小量，我们将rx、ry、rz统统当做0带入原始的TransformToStart()函数中，得到的就是推导出来的结果。所以这里即使不改动代码也能凑合着用。

Gauss-Newton优化算法迭代求解需要的Jacobian矩阵在另一节给出，原始代码对Jacobian矩阵的求解不准确，是否使用IMU也会导致Jacobian矩阵发生变化。

8、integrateTransformation()累计相对位姿

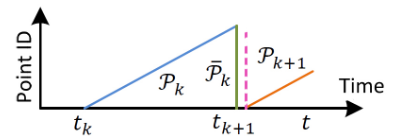
本节点的优化变量是transformSum[]，它是一个帧间相对量，本函数将相对量累积，获得第一帧或者说world系下该帧的位姿。先考虑不使用IMU的情况，根据估计出来的transformCur[]可以获得当前帧结束时刻到当前帧起始时刻的变换$T_{cur-end}^{cur-start}$，$T_{pre-end}^{world}$是上一帧点云结束点时刻到world坐标系的位姿变换，这个函数将其累积：
$$
T_{cur-end}^{world} = T_{pre-end}^{world}T_{cur-end}^{cur-start}
$$
若假设当期帧起始点时刻就是上一帧结束点时刻，这个变换就是完全正确的，实际上这个存在误差：

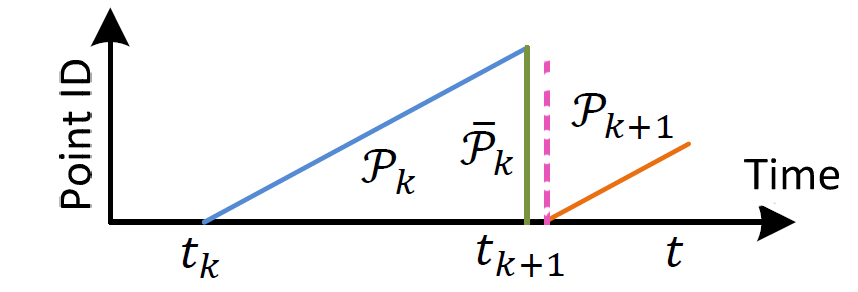
看过LOAM的论文我们知道，上一帧点云处理完毕后被投影到了上一帧点云结束点时刻，就是上图中的绿色的点云，当前帧点云是以绿色的点云为参考的，所以本来求解的就是当前帧结束点时刻到上一帧结束点时刻（不是当前帧起始点时刻）的位姿变换，这样看我们应该这样计算时间比例因子：
$$
s = \frac{t-t_{pre-last}}{t_{cur-last}-t_{pre-last}}
$$
只是有时候我们只有点云的时间戳，没有一帧点云的起始时刻、终止时刻的具体信息，LeGo-LOAM做了个折中吧。

考虑使用IMU的情况，transformCur[]中的旋转是一个小量，优化出来的旋转实际上是将粉色的点云向绿色的点云对齐，这时候经过AccumulateRotation()函数，我们将这个相对旋转变换到了全局坐标系下。但是，这时的旋转是当前帧的起始点到全局坐标系的变换，而我们要得到的是当前帧的结束点到全局坐标系的变换，这也就是PluginIMURotation()函数完成的功能。

PluginIMURotation()函数使用到了IMU的数据，它需要当前帧点云起始激光点相对于惯性系的orientation、当前帧点云最后一个激光点相对于惯性系的orientation。所以这里的公式是：
$$
T_{cur-end}^{world} = T_{pink}^{world}(T_{cur-start}^{n})^{-1}T_{cur-end}^{n}
$$
给我的感觉是，使用IMU后，旋转部分激光只是计算一丢丢，其他都是靠IMU补偿的。

9、发布里程计信息、点云信息

publishOdometry()函数将累积的相对姿态，也就是world坐标系下的姿态publish出去。

publishCloudsLast()函数将本帧处理完的点云投影到结束点时刻，构建kd-tree供给下一帧查询最近点使用，并将去畸变后的点云发布出去。这个函数中的TransformToEnd()在使用IMU时又会出现问题！

TransformToEnd()函数前半部分是实现TransformToStart()的功能，即先将点云变换到一帧点云的起始点时刻、再从起始点时刻变换到结束点时刻。不使用IMU，一切都没问题，若使用IMU，上面已经分析了TransformToStart()函数（即TransformToend()函数的前半段可以凑合着用），但是从起始点时刻再变换到结束点时刻就不对了。出问题的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
rx = transformCur[0];
ry = transformCur[1];
rz = transformCur[2];
tx = transformCur[3];
ty = transformCur[4];
tz = transformCur[5];

// 再从一帧sweep的开始时刻转换到end时刻
// 绕y轴旋转(yaw)
float x4 = cos(ry) * x3 + sin(ry) * z3;
float y4 = y3;
float z4 = -sin(ry) * x3 + cos(ry) * z3;
// 绕x轴旋转(pitch)
float x5 = x4;
float y5 = cos(rx) * y4 - sin(rx) * z4;
float z5 = sin(rx) * y4 + cos(rx) * z4;
// 绕z轴旋转(roll)
float x6 = cos(rz) * x5 - sin(rz) * y5 + tx;
float y6 = sin(rz) * x5 + cos(rz) * y5 + ty;
float z6 = z5 + tz;

还是那句话，使用IMU时transformCur[]中的旋转项是一个小量，这里用到的旋转应该是$(T_{cur-end}^{n})^{-1}T_{cur-start}^{n}$（参考PluginIMURotation()函数）中的旋转项。

10、总结

这里我按照论文中的思路分析代码，我能保证的是不使用IMU时的分析没有问题，使用IMU时按照当期帧点云投影到当前帧结束点时刻，发现有些函数不是那么正确。也可能代码不是按照论文中的思路来理解，例如一帧点云中去掉旋转的部分投影到一帧的起始时刻，平移的部分投影到一帧的结束时刻等，若有小伙伴分析的明明白白，能和代码一一对应，还请指点一二。后续我会一一验证，暂时罗列出来给自己做一个标记。

  1. 点云时间戳不在点云起始点怎么办？

若不使用IMU，点云的时间戳在一帧点云的起始、中间、结束时刻都不要紧，因为时间比例因子与时间戳无关！但是使用IMU后，若还想保持原有点云的去畸变方式，就需要知道点云的起始时刻以及一帧点云的采样时间（用来寻找时间范围内的IMU数据），若点云的时间戳在一帧点云的中间，如KITTI数据集，就得根据这个时间戳近似一个起始时刻的时间戳来使用。这只要更改adjustDistortion()函数中比较时间戳的那段代码。

  1. IMU如何使用？
    • IMU频率必须大于Lidar频率，IMU必须可以直接提供orientation；
    • IMU和Lidar的坐标系和KITTI数据集中的保持一致;
    • Lidar的时间戳是在一帧点云的起始点处;（不使用IMU，Lidar时间戳可以不满足这个要求）；
    • 更改TransformToStart()、TransformToEnd()函数；
    • 更改calculateTransformation()中Jacobian的求解；
  2. 可优化的点？
    • 若准确知道一帧点云的起始时刻和结束时刻，可按照第8节中的公式求解时间比例因子，真正求解当前帧点云结束点到上一帧点云结束点时刻的位姿变换；
    • updateInitialGuess()中初始值的赋予。

11、不解之谜

发布Odomntry时候，为什么要取两次负号？

1
2
3
4
5
6
7
8
// 发布transformSum到里程计消息
geometry_msgs::Quaternion geoQuat = tf::createQuaternionMsgFromRollPitchYaw(transformSum[2], -transformSum[0], -transformSum[1]);
laserOdometry.header.stamp = cloudHeader.stamp;
// TODO::这样做的意义是什么？
laserOdometry.pose.pose.orientation.x = -geoQuat.y;
laserOdometry.pose.pose.orientation.y = -geoQuat.z;
laserOdometry.pose.pose.orientation.z = geoQuat.x;
laserOdometry.pose.pose.orientation.w = geoQuat.w;

退化运动的处理？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// 求解对称矩阵matAtA的特征值/特征向量，特征值按照降序排序
cv::eigen(matAtA, matE, matV);
matV.copyTo(matV2);
isDegenerate = false;
float eignThre[6] = {10, 10, 10, 10, 10, 10};
for (int i = 5; i >= 0; i--) {
    // 如果第一次迭代时，matAtA的特征值小于一个阈值，认为发生了退化运动
    if (matE.at<float>(0, i) < eignThre[i]) {
        for (int j = 0; j < 6; j++) {
            matV2.at<float>(i, j) = 0;
          }
          isDegenerate = true;
        } else {
          break;
        }
      }
      matP = matV.inv() * matV2;
    }
    // 如果发生退化，TODO::使用预测矩阵P计算？why?
    if (isDegenerate) {
      cv::Mat matX2(6, 1, CV_32F, cv::Scalar::all(0));
      matX.copyTo(matX2);
      matX = matP * matX2;
    }
听说打赏我的人，最后都找到了真爱。