IMU预积分(二)——线性视觉惯导初始化
这篇文章紧跟IMU预积分(一),主要记录2012年那篇经典的预积分论文中的初始化部分。
1、以首帧位姿为参考坐标系
IMU预积分(一)中,我们推导出了一种将若干惯性测量值集成到载体坐标系下的方法,这种方法可在载体初始条件未知的情况下进行积分,得出的一个重要公式如下:
$$
\begin{array}{l}
p_{t2}^n=p_{t1}^n+(t_2-t_1)v_{t1}^n+\frac{1}{2}(t_2-t_1)^2g^n+C_{bt1}^n\Delta p_{t2}^{+t1} \\
v_{t2}^n=v_{t1}^n+(t_2-t_1)g^n+C_{bt1}^n\Delta v_{t2}^{t1} \\
\phi_{t2}^{n} = EulerFromDCM(C_{bt1}^n\Delta C_{bt2}^{bt1}) –旋转矩阵到欧拉角
\end{array} \tag{1.1}
$$
然而,当预积分的观测数据融合到导航框架下,这些初始条件仍然是必须的,正如公式(1.1)所描述的,$p_{ta}^n,v_{t1}^n,C_{bt1}^n$在导航框架下仍是需要估计的。全球导航参考坐标系例如北京54坐标系等常用做惯性导航的导航坐标系,尤其有GPS观测时,在这个坐标系下重力是已知的,但还需要知道初始帧在导航坐标系中的位置、姿态和速度。对于大多数的SLAM应用,以起始帧作为导航坐标系就足够了,当没有绝对位姿观测时,甚至是必须的。下图展示了以首帧为参考坐标系的惯性导航:
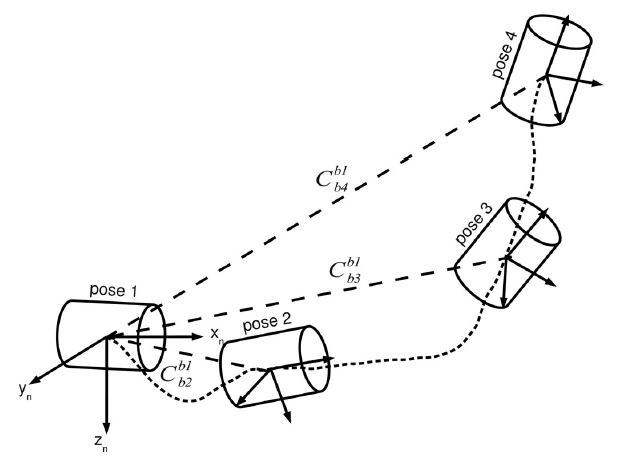
在全局参考坐标系下,估计初始条件的主要问题或者难点来自旋转矩阵带来的非线性。若以第一帧为导航的参考坐标系,则载体的初始姿态就是完全确定的了(平移是0,旋转是单位矩阵),这消除了非线性的影响,然而,由于使用了方向任意的参考坐标系,在这个参考坐标系下重力是未知的。这种方法的优点在于对重力的估计是线性的,对初始条件中的旋转估计则不是。
就是说,以全局参考坐标系为导航坐标系时,重力是已知的,但是初始的位置、速度、旋转需要估计,其中对旋转的估计是非线性的;以第一帧为导航坐标系时,初始的位置、旋转是完全确定的,但可以用线性的方法估计初始速度、重力。
2、初始速度估计
重新排列公式(1.1)中的第一个公式,可以看出载体的初始速度是可以观测的:
$$
v_{t1}^n=\frac{p_{t1}^n-p_{t2}^n+C_{bt1}^n \Delta p_{t2}^{+t1}+\frac{1}{2}(t_2-t_1)^2g^n}{-(t_2-t_1)} \tag{1.2}
$$
因此,给定导航坐标系下的重力矢量以及另一个传感器(如相机)对两个位姿之间的相对位置估计,则平台的初始速度可以以线性的方式获取。可以看出,初始速度可观测的一个标准是能够估计出导航坐标系下的重力矢量。
3、重力矢量的估计
使用两个连续的位置预积分,一个速度预积分,需要的公式如下:
$$
\begin{array}{l}
p_{t2}^n=p_{t1}^n+(t_2-t_1)v_{t1}^n+\frac{1}{2}(t_2-t_1)^2g^n+C_{bt1}^n\Delta p_{t2}^{+t1} \\
p_{t3}^n=p_{t2}^n+(t_3-t_2)v_{t2}^n+\frac{1}{2}(t_3-t_2)^2g^n+C_{bt2}^n\Delta p_{t3}^{+t2} \\
v_{t2}^n=v_{t1}^n+(t_2-t_1)g^n+C_{bt1}^n\Delta v_{t2}^{t1} \\
\end{array}\tag{1.3}
$$
将速度方程带入第二个位置方程:
$$
\begin{aligned}
p_{t 3}^{n}=& p_{t 2}^{n}+(t 3-t 2)\left(v_{t 1}^{n}+(t 2-t 1) g^{n}+C_{b t 1}^{n} \Delta v_{t 2}^{t 1}\right) \\
&+\frac{1}{2}(t 3-t 2)^{2} g^{n}+C_{b t 2}^{n} \Delta p_{t 3}^{+t 2} \\
=& p_{t 2}^{n}+(t 3-t 2)\left(v_{t 1}^{n}+C_{b t 1}^{n} \Delta v_{t 2}^{t 1}\right)+C_{b t 2}^{n} \Delta p_{t 3}^{+t 2} \\
&+(t 3-t 2)\left(\frac{1}{2}(t 3-t 2)+(t 2-t 1)\right) g^{n}
\end{aligned} \tag{1.4}
$$
将公式(1.3)中第一个位置方程中的$v_{t1}^n$分离,带入公式(1.4)并从中分离出重力矢量:
$$
g^{n}=\frac{p_{t 2}^{n}-p_{t 3}^{n}+(t 3-t 2)\left(\left(\frac{p_{t 1}^{n}-p_{t 2}^{n}+C_{b t 1}^{n} \Delta p_{t 2}^{+t 1}}{(t 2-t 1)}\right)+C_{b t 1}^{n} \Delta v_{t 2}^{t 1}\right)+C_{b t 2}^{n} \Delta p_{t 3}^{+t 2}}{(t 3-t 2)\left(\frac{1}{2}(t 3-t 2)+\frac{3}{2}(t 2-t 1)\right)}\tag{1.5}
$$
这一推导表明,仅在三帧图像的相对位置被估计之后,就可以线性地获得载体的初始速度和重力矢量的估计值。重力矢量可观测带来的一个益处是,利用这个估计,可以提取出载体在导航系下的绝对横摇角和俯仰角。虽然此时我们有了一个重力矢量的估计,但是它并不准确,所以一些VIO在后端优化中也加入了对重力矢量的估计。VINS-mono对重力矢量的refine很巧妙,之后会记录。

