VINS中的视觉残差

1、视觉残差定义

VINS中的重投影是在归一化相机平面中完成的，重投影误差是估计值与测量值的差，有如下的形式：
$$
r_c=
\left[
\begin{array}{c}
\frac{X_c}{Z_c}-u \\
\frac{Y_c}{Z_c}-v \\
\end{array}
\right]
\tag{1}
$$

其中优化变量是特征点在相机坐标系下的空间坐标$(X_c,Y_c,Z_c)$，$(u,v)$是特征点在归一化相机平面上的测量值。实际在VINS的优化变量中，VINS并未优化路标点的所有维度，只对特征点的逆深度做了优化，相机坐标系中的点与归一化平面中的点有如下的关系:
$$
\left[\begin{array}{c}X_c\\Y_c\\Z_c\end{array}\right]
=
Z_c\left[\begin{array}{c}u\\v\\1\end{array}\right]
=
\frac{1}\lambda\left[\begin{array}{c}u\\v\\1\end{array}\right]
\tag{2}
$$
其中$\lambda$就是特征点的逆深度。VINS中具体的重投影误差可做如下推导：

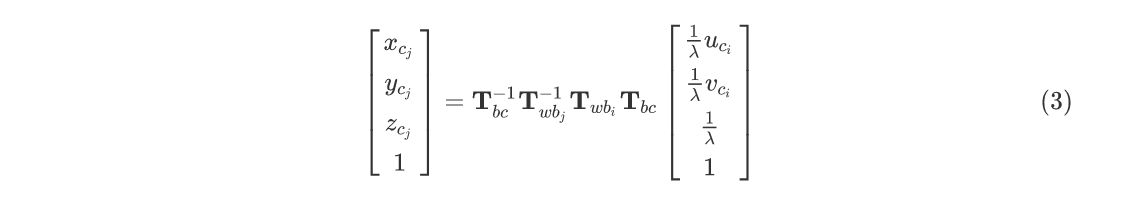
它表示在第$i$帧归一化平面的观测凭借运动关系，投影到第$j$帧相机坐标系下的坐标，则视觉重投影误差为：
$$
r_c=
\left[
\begin{array}{c}
\frac{x_{cj}}{z_{cj}}-u_{cj} \\
\frac{y_{cj}}{z_{cj}}-v_{cj} \\
\end{array}
\right]
\tag{4}
$$
视觉残差包含的优化变量有两个时刻的姿态$T_{wbj}、T_{wbi}$、外参$T_{bc}$、特征点的逆深度$\lambda$。使用逆深度的优点在于，在极线搜索和块匹配中，我们假设深度值满足高斯分布。然而仔细想想会发现，深度的正态分布确实存在一些问题：

.实际想表达的是：这个场景深度大概是5-10米，可能有一些更远的点，但近处肯定不会小于相机焦距（或者认为深度不会小于0）.这个分布并不是像高斯分布那样，形成一个对称的形状。它的尾部可能稍长，而负数区域则为零。
在一些室外应用中，可能存在距离非常远，乃至无穷远处的点。我们的初始值中难以覆盖这些点，并且用高斯分布描述他们会有一些数值计算上的困难。
在Bundle Ajustment中，参数空间通常呈现出高维度、非线性的特点。其中对于3D特征点的优化占据了大量的运算量。然而当特征点的距离很远时，该特征点带来的误差就会很大，代价函数需要对该特征点进行较大幅度的调整才能进一步降低代价函数。

于是，逆深度应运而生。人们在仿真中发现，假设深度的倒数（也就是逆深度），为高斯分布是比较有效的。

2、VINS中的特征点管理

谈到视觉误差，我们有必要了解实际代码中VINS是如何管理特征点的，以便于进行视觉重投影误差的计算，VINS中描述特征点主要使用了两个类，定义在feature_manager.h 中：

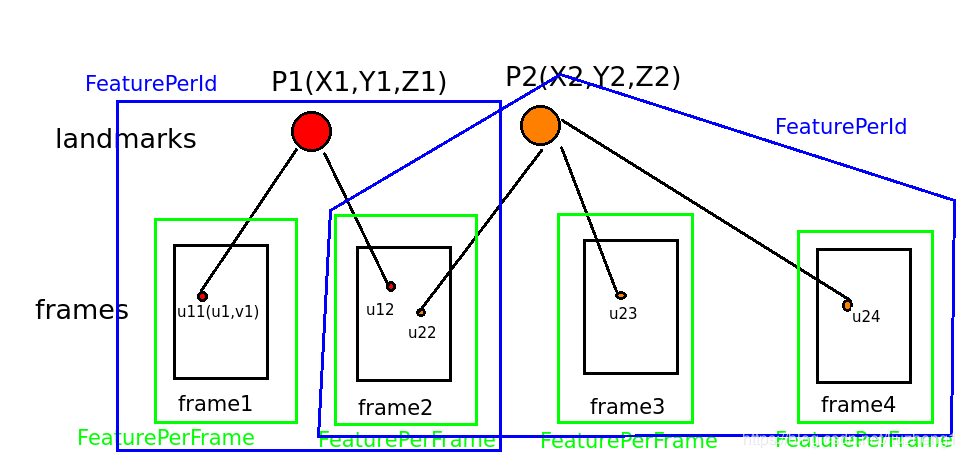
上图中绿色的框和蓝色的框形象地说明了这两个类的关系，FeaturePerFrame类定义如下，它描述了绿色的框表示的信息。

/**
 * @brief 3D特征点投影到每一帧上产生的信息
 */
class FeaturePerFrame
{
public:
  FeaturePerFrame(const Eigen::Matrix<double, 7, 1> &_point, double td)
  {
    point.x() = _point(0);
    point.y() = _point(1);
    point.z() = _point(2);
    uv.x() = _point(3);
    uv.y() = _point(4);
    velocity.x() = _point(5);
    velocity.y() = _point(6);
    cur_td = td;
  }
  double cur_td;      //imu-camera的不同步时的相差时间
  Vector3d point;     //特征点空间坐标
  Vector2d uv;        //特征点映射到该帧上的图像坐标
  Vector2d velocity;  //特征点的跟踪速度
  double z;
  bool is_used;
  double parallax;
  MatrixXd A;
  VectorXd b;
  double dep_gradient;
};

FeaturePerId是绿色框的集合，表示了一个路标点的所有信息，因为VINS的前端使用光流法，蓝色的框包含的一定是连续的几个绿色的框，代码如下：

/**
 * @brief 一个3D路标点
 */
class FeaturePerId
{
public:
  const int feature_id;                         // 特征点ID
  int start_frame;                              // 从哪一帧开始被观测
  vector<FeaturePerFrame> feature_per_frame;    // 此路标点被哪些帧观测,假如一个3Dlandmark被1，2，3帧中被观测到，
                                                // FeaturePerFrame存储的是3D点在对应帧中的像素坐标等信息。由于是光流跟踪，被观测的帧一定是连续的
  int used_num;                                 // 被观测到的次数，等于feature_per_frame.size()
  bool is_outlier;
  bool is_margin;
  double estimated_depth;                       // 特征点在第一次观测到它的帧中的深度
  int solve_flag;                               // 0 haven't solve yet; 1 solve succ; 2 solve fail;

  Vector3d gt_p;

  FeaturePerId(int _feature_id, int _start_frame)
      : feature_id(_feature_id), start_frame(_start_frame),
        used_num(0), estimated_depth(-1.0), solve_flag(0) {}

  int endFrame();
};

3、视觉残差的Jacobian

在后端优化时，我们需要提供残差函数关于优化变量的Jacobian矩阵，视觉残差的Jacobian矩阵推导如下，字写得比较潦草，将就看吧，以下PDF可供下载：

4、参考

1.图像来源https://blog.csdn.net/liuzheng1/article/details/90052050