VINS-Mono初始化

VINS中外参、Bias初始化

我们要知道，视觉与IMU有良好的互补性，IMU可以提高系统处理快速运动的性能，摄像机可以解决慢速运动下IMU的漂移问题。这种单目视觉-惯性系统的主要优点是具有可观测的度量尺度，这让需要有度量尺度的导航任务成为可能，尺度的确定就是在初始化阶段完成的。在IMU预积分(二)——线性视觉惯导初始化中我们分析出预积分需要估计出初始帧的速度、重力，在VINS-Mono中我们也需要完成这项工作。除此之外，VINS-Mono还估计了陀螺仪的bias来提高预积分精度，并且提供了在线外参矫正功能。

所以在VINS-Mono的初始化阶段，我们需要估计出来尺度、速度、重力、陀螺仪零偏、相机与IMU之间的外参，我们逐一来学习VINS-Mono中采用的策略。

1、在线外参矫正

初始化的一个原理就是相机的测量值与IMU的测量值应该是一致的，来看下面的图像：

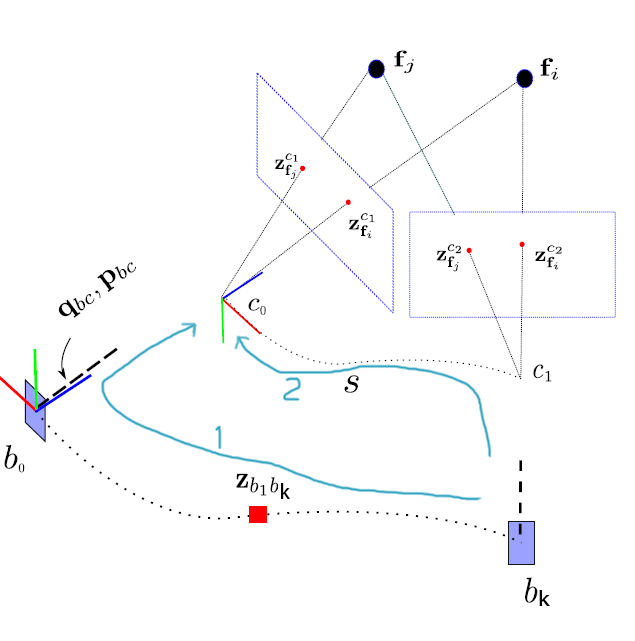
此图表示在两图像帧之间有k个IMU帧，IMU与相机的测量值应该保持一致，只是平移的尺度未统一。按照上图中蓝色的路径，我们可以列出下面这个约束方程：
$$
(T_{c}^{b})^{-1} T_{b_k}^{b_0}= T_{c_1}^{c_0} (T_{c}^{b})^{-1} \tag{1.1}
$$
其中$T$属于特殊欧式群，从中我们分离出旋转项，使用四元数来表示：
$$
(q_{c}^{b})^{-1} \otimes q_{b_k}^{b_0}= q_{c_1}^{c_0} \otimes (q_{c}^{b})^{-1} \tag{1.2}
$$
理论上这个公式是严格成立的，但是噪声的存在致使这个公式不是严格的等于，所以左右两端有一个偏差，VINS-Mono中使用角度误差来表示这个偏差：
$$
\delta R = (R_{c}^{b})^{-1}R_{b_k}^{b_0}R_{c}^{b}(R_{c_1}^{c_0})^{-1} \tag{1.3}
$$
使用公式$tr(R)=1+2cos \theta$，将旋转矩阵误差转换为角度（弧度）误差：
$$
r_{1}^{0} = acos(\frac{tr(\delta R)-1}{2}) \tag{1.4}
$$
这个角度误差会被用作鲁棒核权重来提高求解的稳定性。

将公式（1.2）写成矩阵表示的形式，这利用到了四元数的左乘以及右乘算子，可以参考VINS中IMU残差中的推导或者百度一下：

将多个时刻的线程方程（1.5）累计起来，并加上鲁棒核权重得到：

其中鲁棒核权重如下计算：

这个公式意义也很明确，角度误差大的项占有的权重小。公式（1.6）这个约束方程又是我们熟悉的形式，可以使用来求解。

2、陀螺仪Bias矫正

在估计出来外参或者事先已经标定好相机与IMU的情况下，我们可以估计陀螺仪的Bias了，因为加速度计的bias通常和重力耦合在一块，或者说被重力淹没了，所以VINS中并没有估计加速度计的bias。

VINS-Mono代码中使用的约束是：
$$
\arg \min {\delta \mathbf{b}^{g}} \sum{k \in B}\left|2\left\lfloor\mathbf{q}{c{0} b_{k+1}}^{-1} \otimes \mathbf{q}{c{0} b_{k}} \otimes \mathbf{\gamma}{b{k} b_{k+1}}\right\rfloor_{x y z}\right|^{2} \tag{2.1}
$$
其中$B$是滑动窗口中的帧数量，$b_k$表示滑动窗口中的第$k$帧；此公式与公式（1.3）表示的含义相同，都表示角度误差，只是选择的参考坐标系不同，公式（1.3）的表述形式是$\delta R = \tilde R_{c_1}^{c_0} (R_{c_1}^{c_0})^{-1}$,角度误差的参考坐标系是相机系；公式（2.1）的表述形式是：$\delta q = \tilde{q}_{b_k}^{b_{k+1}} \otimes q_{b_{k+1}}^{b_k}$，角度误差的参考坐标系是IMU系。不同于估计外参$q_c^b$时使用对极约束估计帧间$R_{c_1}^{c_0}$，这里先进行Structure From Motion，之后构建了一个BA优化问题得到更加精确的旋转$R_{c_k}^{c_l}$，所有的旋转都是相对于滑动窗口中的第$l$帧的。

根据估计出的外参数，做一个简单的乘法便可以得到公式（2.1）中需要的变量：
$$
q_{b_k}^{c_l}= q_{c_k}^{c_l} \otimes (q_{c}^{b})^{-1} \tag{2.2}
$$
将公式（2.1）分解，提取出某一帧误差$f_k$：
$$
f_k=2\left\lfloor\mathbf{q}{c{0} b_{k+1}}^{-1} \otimes \mathbf{q}{c{0} b_{k}} \otimes \mathbf{\gamma}{b{k} b_{k+1}}\right\rfloor_{x y z} = 2\left\lfloor\mathbf{q}{b{k+1} b_{k}}\otimes \mathbf{\gamma}{b{k} b_{k+1}}\right\rfloor_{x y z} \tag{2.3}
$$
根据IMU预积分(四)中根据偏差矫正旋转项的预积分，有以下的公式：
$$
\gamma_{b_{k+1}}^{b_{k}} \approx \hat{\gamma}{b{k+1}}^{b_{k}} \otimes\left[\begin{array}{c}
1 \\
\frac{1}{2} \mathbf{J}{b{kg}}^{\gamma} \delta \mathbf{b}{kg}
\end{array}\right] \tag{2.4}
$$
将公式（2.4）带入公式（2.3）我们得到：
$$
f_k= 2\left\lfloor\mathbf{q}{b_{k+1} b_{k}}\otimes \hat{\gamma}{b{k+1}}^{b_{k}} \otimes\left[\begin{array}{c}
1 \\
\frac{1}{2} \mathbf{J}{b{kg}}^{\gamma} \delta \mathbf{b}{kg}
\end{array}\right]\right\rfloor{x y z} \tag{2.5}
$$
我们认为视觉测量值是非常准确的，所以视觉测量得到的$q_{b_{k+1 b_k}}$与预积分的真实值$\hat{\gamma}_{b_{k+1}}^{b_{k}} $相等，所以这个误差实际为：
$$
f_k= 2\left\lfloor\left[\begin{array}{c}
1 \\
\mathbf 0
\end{array}\right] \otimes\left[\begin{array}{c}
1 \\
\frac{1}{2} \mathbf{J}{b{kg}}^{\gamma} \delta \mathbf{b}{kg}
\end{array}\right]\right\rfloor{x y z}
$$

$$
f_k=\mathbf{J}{b{kg}}^{\gamma} \delta \mathbf{b}_{kg} \tag{2.6}
$$

这是一个线性方程约束，VINS-Mono中认为初始化时滑窗中所有帧的陀螺仪零偏变化量相同，使用高斯牛顿法可以解出公式（2.1）的最优解为：
$$
\sum_{k \in B} (\mathbf{J}{b{kg}}^{\gamma T}\mathbf{J}{b{kg}}^{\gamma}) \Delta b_g = -\sum_{k \in B}(\mathbf{J}{b{kg}}^{\gamma T}f_k) \tag{2.7}
$$
这个方程的系数矩阵是对称正定的，可以使用Cholesky分解求解$\Delta b_g$，之后更新陀螺仪的零偏，重新计算得到更加准确的预积分项。

3、尺度、速度、重力的恢复

在第1、2部分的推导中，我们注意到了，只将IMU预积分得到的旋转项与视觉得到的旋转项对齐便可以恢复出外参、陀螺仪的Bias。这里我们还要恢复出尺度、速度、重力，速度和重力在IMU预积分位移项、速度项中出现，尺度问题只影响平移向量，也是出现在IMU预积分的位移项，根据IMU预积分(四)中的内容，我们很容易得到下面的方程：
$$
\begin{aligned}
&\alpha_{b_j}^{b_i}=q_{w}^{b_i}(p_{b_j}^w-p_{b_i}^w-v_i^w \Delta t+\frac{1}{2}g^w \Delta t^2) \\
&\beta_{b_j}^{b_i}=q_w^{b_i}(v_j^w-v_i^w+g^w \Delta t)
\end{aligned} \tag{3.1}
$$
在IMU预积分(二)中我们分析了以第一帧相机或者IMU为世界坐标系带来的好处，VINS-Mono也采用了这个策略，以第一帧相机坐标系为世界坐标系公式（3.1）同样成立，我们换一种字母来表示，$k$为滑动窗口中的第$k$帧，$b_k$表示第$k$个IMU帧：
$$
\begin{aligned}
&\alpha_{b_{k+1}}^{b_{k}}=R_{c_0}^{b_k}(p_{b_{k+1}}^{c_0}-p_{b_k}^{c_0}-R_{b_k}^{c_0}v_k^{b_k} \Delta t+\frac{1}{2}g^{c_0} \Delta t^2) \\
&\beta_{b_{k+1}}^{b_{k}}=R_{c_0}^{b_k}(R_{b_{k+1}}^{c_0}v_{k+1}^{b_{k+1}}-R_{b_k}^{c_0}v_k^{b_k}+g^{c_0} \Delta t)
\end{aligned} \tag{3.2}
$$
注意：这里没有将速度转换到$c_0$帧下，这是因为我们的预积分都是在body系下完成的，直接估计出body系下的速度显然是方便了我们对速度预积分项的计算。同时注意到公式（3.2）中体现出来了要初始化的速度$v_{k+1}^{b_{k+1}}、v_k^{b_k}$、重力$g^{c_0}$，但是尺度因子没有体现出来，这就需要我们对平移向量$p_{b_{k+1}}^{c_0}、p_{b_k}^{c_0}$进行处理了。这个处理也简单粗暴，直接在非米制单位的轨迹上乘一个尺度因子s将其变为米制单位，即$p_{b_{k+1}}^{c_0} = s\bar{p}{b\{k+1}}^{c_0},p_{b_{k}}^{c_0} = s\bar{p}_{b_{k}}^{c_0}$，其中$\bar{p}_{b_{k+1}}^{c_0},\bar{p}_{b_{k}}^{c_0}$是可以通过视觉SFM获得的尺度不确定的平移向量，方法如下：(原理$T_{b_k}^{c_0} = T_{c_k}^{c_0}(T_c^b)^{-1}$，展开可获得如下的方程)
$$
\begin{aligned}
&s\bar{p}{b{k+1}}^{c_0} = s\bar{p}{c{k+1}}^{c_0} - R_{c_{k+1}}^{c_0}(R_c^b)^{-1}p_c^b\\
&s\bar{p}{b{k}}^{c_0} = s\bar{p}{c{k}}^{c_0} - R_{c_{k}}^{c_0}(R_c^b)^{-1}p_c^b
\end{aligned} \tag{3.3}
$$
将这个方程带入到公式（3.2）的第一个方程中得到：
$$
\alpha_{b_{k+1}}^{b_{k}} = sR_{c_0}^{b_k}(\bar{p}{c{k+1}}^{c_0} - \bar{p}{c{k}}^{c_0}) - R_{c_0}^{b_k}R_{b_{k+1}}^{c_0}p_c^b+p_c^b - v_k^{b_k} \Delta t+\frac{1}{2}R_{c_0}^{b_k}g^{c_0} \Delta t^2 \tag{3.5}
$$
将公式（3.5）与公式（3.3）第二个公式重新整理，将待估计变量放到方程右边，有：
$$
\hat{z}{b{k+1}}^{b_k}=
\left[\begin{array}{c}
\hat{\alpha}{b{k+1}}^{b_{k}}- p_c^b + R_{c_0}^{b_k}R_{b_{k+1}}^{c_0}p_c^b \\
\hat{\beta}{b{k+1}}^{b_k}
\end{array}\right]{6\times 1}
=
H{b_{k+1}}^{b_k}\mathcal{X}{I}^{k}+\mathbf{n}{b_{k+1}}^{b_{k}} \tag{3.6}
$$
公式（3.6）中：
$$
\begin{aligned}
&\mathcal{X}{I}^{k}=\left[{v}{k}^{b_{k}}, {v}{k+1}^{b{k+1}}, {g}^{c_{0}}, s\right]^{\top} \\
&H_{b_{k+1}}^{b_k} =
\left[\begin{array}{cccc}
-\mathbf{I} \Delta t & \mathbf{0} & \frac{1}{2} R_{c_0}^{b_k} \Delta t^{2} & R_{c_0}^{b_k}\left(\overline{\mathbf{p}}{c{k+1}}^{c_{0}}-\overline{\mathbf{p}}{c{k}}^{c_{0}}\right) \\
-\mathbf{I} & {R}{c_0}^{b_k} R{b_{k+1}}^{c_0} & R_{c_0}^{b_k}\Delta t & \mathbf{0}
\end{array}\right]{6 \times 10}
\end{aligned} \tag{3.7}
$$
其中$\hat{\alpha}$表示预积分的真实值，使用真实值加噪声项$\mathbf{n}$可使公式（3.6）恒成立，由推导过程可知这个噪声项来自于预积分项中的噪声项，根据IMU预积分(三)中IMU预积分的噪声项服从零均值的高斯分布，所以公式（3.6）中的噪声$\mathbf{n}$也是高斯白噪声。故我们可以使用最大似然概率进而转换为最小二乘来求解这个线性方程的最优解。对滑动窗口中的所有帧建立同样的约束，则我们要做的是：
$$
\min _{\mathcal{X}{I}} \sum_{k \in \mathcal{B}}\left|\hat{ \mathbf {z}}{b{k+1}}^{b_{k}}-\mathbf{H}{b{k+1}}^{b_{k}} \mathcal{X}{I}\right|^{2} \tag{3.8}
$$
注意此$\mathbf{H}$非彼$H$，它的维度已经扩充了，只不过扩充的地方元素都是0，同理$\mathbf{z}$也是，其中整个滑窗总的状态量是：
$$
\mathcal{X}{I} = \left[v_{b_{0}}^{b_{0}}, v_{b_{1}}^{b_{1}}, \cdots v_{b_{N}}^{b_{N}},g^{c_{0}}, s\right] \tag{3.9}
$$
这个公式与公式（2.7）的求解原理一致。当然我们也可以最小化加权最小二乘，这就需要公式（3.6）的不确定性关系（信息矩阵）了，这个不确定信息是由IMU预积分造成的，我们可以从IMU预积分的协方差矩阵$F$中提取出对应块来实现。