IMU预积分(四)——VINS-mono中的预积分
有了前三篇预积分文章的基础,理解VINS-mono中的预积分就水到渠成了。VINS-mono与2015年流行上的预积分的区别是:VINS-mono采用的参数化方式不同,离散化手段不同。除此之外,要实现的目的是一致的。
通常情况下VINS-mono采用的硬件,IMU 测量频率为几百赫兹 ,摄像机测量频率几十赫兹 。如下图所示,在两次摄像机采样时刻k 与k+1 之间有多个IMU 测量值,但是原始测量数据不方便直接作为约束载体位姿的边,故使用预积分技巧将多个IMU 测量值转化为一个整体观测量。

在中,我们说使用预积分需要完成四件事,我们来看看VINS-mono是如何实现的:
1、IMU测量模型
为了本篇文章的完整性,这里将中的IMU预积分模型搬来:

其中$\mathbf{b_g}$与$\mathbf{b_a}$是随时间缓慢变化的陀螺仪与加速度计的bias;在VINS-mono中被建模为随机游走——即$\mathbf{b_g}$与$\mathbf{b_a}$的导数服从高斯分布:
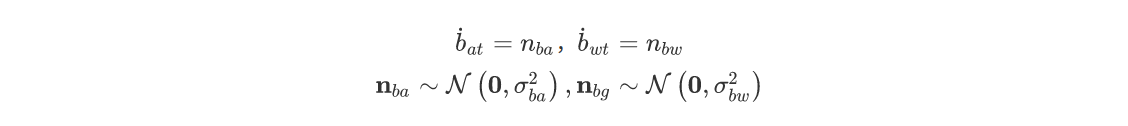
$\eta_{g}$与$\eta_{a}$建模为服从高斯分布的白噪声:
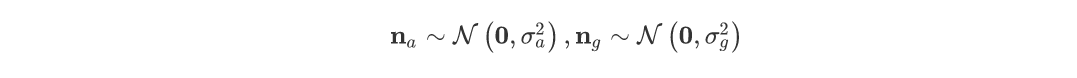
重力$g^w$前的符号是正或者负没有影响的,只要我们明确加速度计敏感到的加速度包含了反向重力加速度的比力。例如我们选取水平地理坐标系东北天,则这里$g^w=[0,0,9.8]$。
2、预积分递推公式
根据牛顿第二定律,在世界坐标系下从第$i$时刻的PVQ对IMU测量值进行积分,得到第$j$时刻的PVQ:
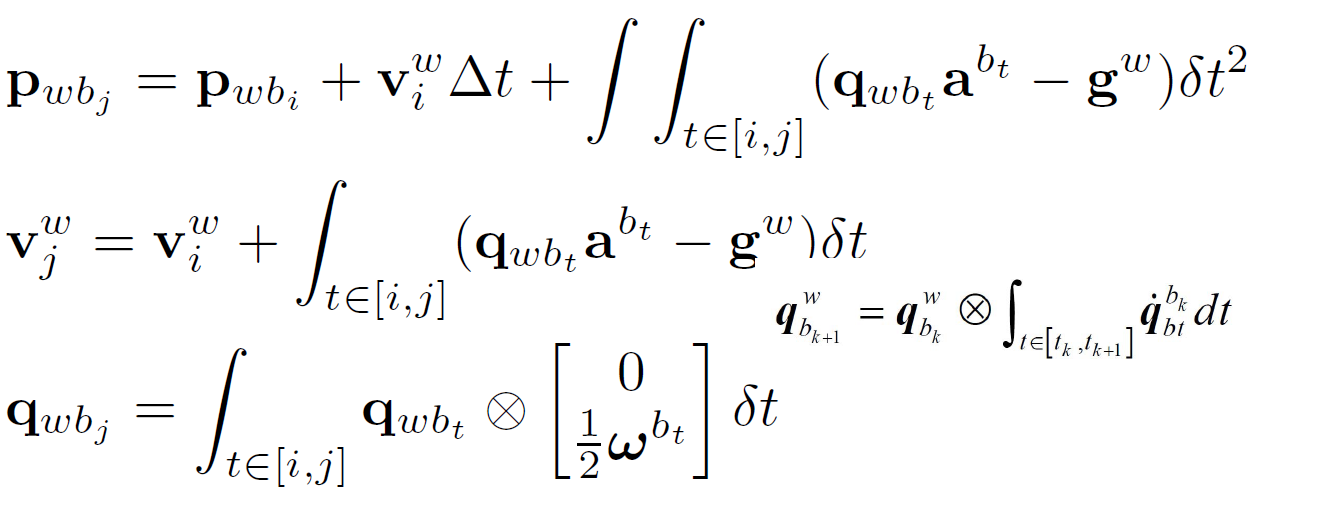
这里的$a^{bt}$,$w^{bt}$是带有噪声的IMU测量值,$\Delta t$是两帧图像之间的时间差,$\delta t$是连续两IMU帧的时间差,只需要做一个简单的变换,我们就可从积分项中将绝对位姿解耦:

连续形式的预积分项就是下面:
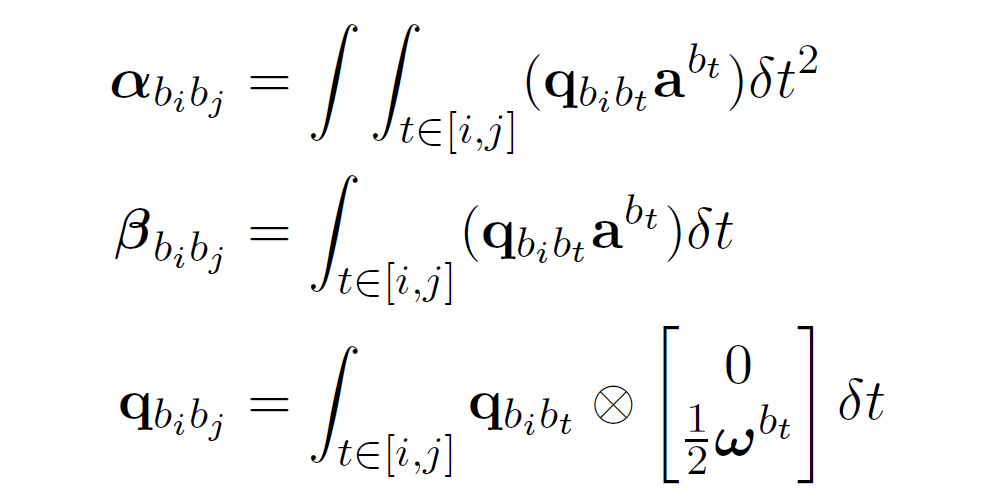
使用中值积分离散化预积分项:

在VINS-mono中,沈老师使用四元数描述旋转,由于四元数的过参数化(实际三个参数就可以表示旋转),所以在表达旋转或者说是在优化变量中使用的是四元数的虚部,但是在实际计算推导过程中为了避免奇异性使用的是四元数与方向余弦矩阵。
3、预积分项不确定性的计算
在中,我们得到状态误差的线性递推关系具有如下的形式:
$$
\delta x_k = F\delta x_{k-1}+Gn_{k-1}
$$
接下来推导在中值积分下的$F$与$G$矩阵:
4、Bias偏差修正
使用下面的泰勒展开线性地修正bias带来的偏差:
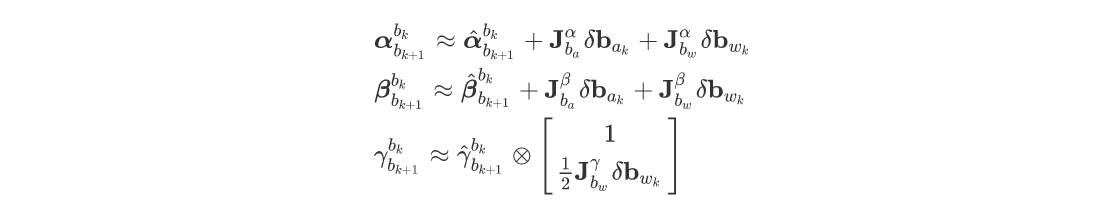
这个公式的重点在于求解那五个雅可比矩阵,这五个雅克比矩阵是第5小节残差雅克比矩阵中的对应子块(只相差了符号),所以推导过程统一放在第5小节。
5、IMU残差项及其雅克比矩阵
VINS-mono中融合了IMU与相机,IMU残差如下:
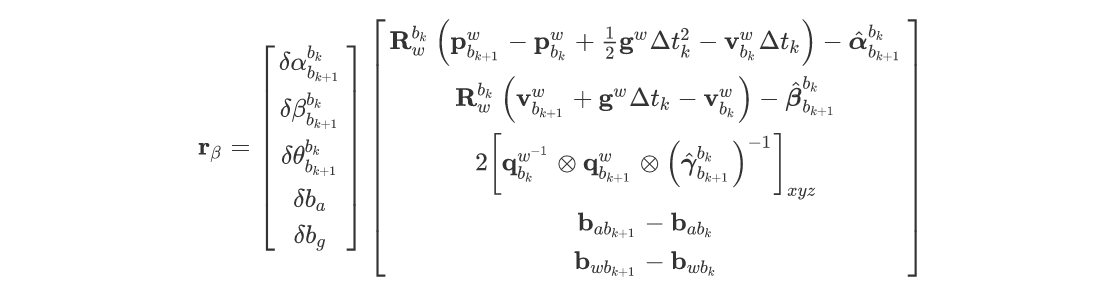
这些残差是由相机的测量与IMU预积分的差值构成的,使用非线性优化的手段去估计最优解,我们需要求解IMU残差关于待优化变量的雅克比矩阵,详细的推导如下:

